Question Number 128068 by benjo_mathlover last updated on 04/Jan/21
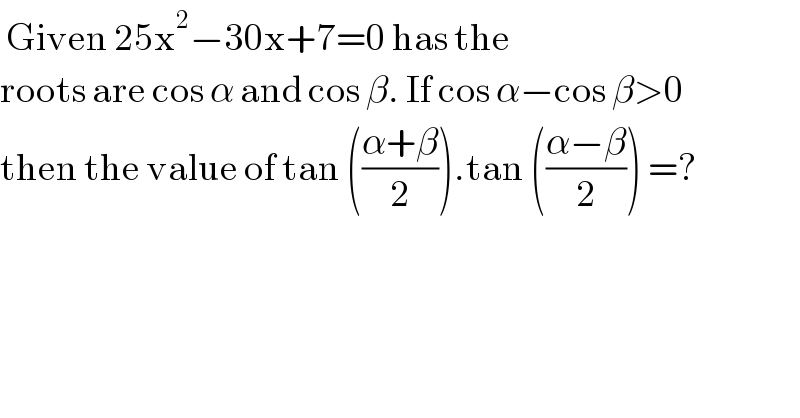
$$\:\mathrm{Given}\:\mathrm{25x}^{\mathrm{2}} −\mathrm{30x}+\mathrm{7}=\mathrm{0}\:\mathrm{has}\:\mathrm{the} \\ $$$$\mathrm{roots}\:\mathrm{are}\:\mathrm{cos}\:\alpha\:\mathrm{and}\:\mathrm{cos}\:\beta.\:\mathrm{If}\:\mathrm{cos}\:\alpha−\mathrm{cos}\:\beta>\mathrm{0} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right).\mathrm{tan}\:\left(\frac{\alpha−\beta}{\mathrm{2}}\right)\:=? \\ $$
Answered by bemath last updated on 04/Jan/21

$$\:\mathrm{let}\:\frac{\alpha+\beta}{\mathrm{2}}=\mathrm{x}\:\wedge\:\frac{\alpha−\beta}{\mathrm{2}}=\mathrm{y} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{tan}\:\mathrm{x}.\mathrm{tan}\:\mathrm{y}\:=\:\frac{\mathrm{2sin}\:\mathrm{xsin}\:\mathrm{y}}{\mathrm{2cos}\:\mathrm{xcos}\:\mathrm{y}} \\ $$$$\:\:\:=\:\frac{\mathrm{cos}\:\left(\mathrm{x}−\mathrm{y}\right)−\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)}{\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{cos}\:\left(\mathrm{x}−\mathrm{y}\right)} \\ $$$$\:=\:\frac{\mathrm{cos}\:\beta−\mathrm{cos}\:\alpha}{\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta}\:=\:\frac{\mathrm{cos}\:\beta−\mathrm{cos}\:\alpha}{\left(\frac{\mathrm{6}}{\mathrm{5}}\right)} \\ $$$$\:=\:−\frac{\mathrm{5}}{\mathrm{6}}\sqrt{\left(\mathrm{cos}\alpha−\mathrm{cos}\:\beta\right)^{\mathrm{2}} \:} \\ $$$$\:=−\frac{\mathrm{5}}{\mathrm{6}}\sqrt{\left(\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta\right)^{\mathrm{2}} −\mathrm{4cos}\:\alpha\mathrm{cos}\:\beta} \\ $$$$\:=−\frac{\mathrm{5}}{\mathrm{6}}\:\sqrt{\frac{\mathrm{36}}{\mathrm{25}}−\frac{\mathrm{28}}{\mathrm{25}}}\:=\:−\frac{\mathrm{5}}{\mathrm{6}}×\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{5}} \\ $$$$\:=−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Jan/21
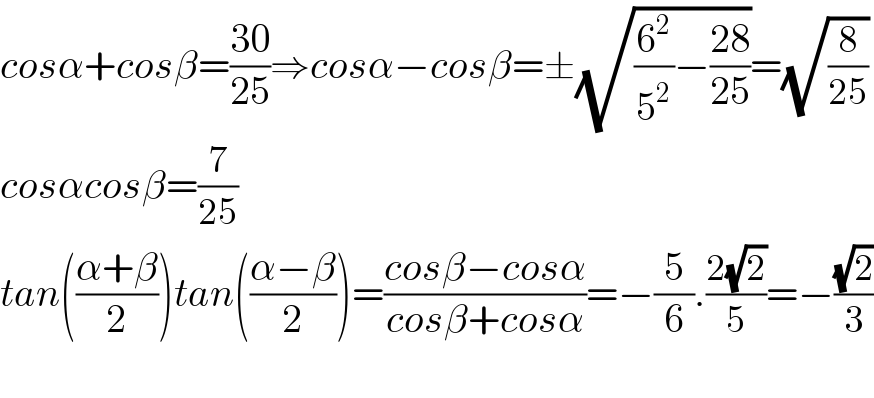
$${cos}\alpha+{cos}\beta=\frac{\mathrm{30}}{\mathrm{25}}\Rightarrow{cos}\alpha−{cos}\beta=\pm\sqrt{\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{5}^{\mathrm{2}} }−\frac{\mathrm{28}}{\mathrm{25}}}=\sqrt{\frac{\mathrm{8}}{\mathrm{25}}} \\ $$$${cos}\alpha{cos}\beta=\frac{\mathrm{7}}{\mathrm{25}} \\ $$$${tan}\left(\frac{\alpha+\beta}{\mathrm{2}}\right){tan}\left(\frac{\alpha−\beta}{\mathrm{2}}\right)=\frac{{cos}\beta−{cos}\alpha}{{cos}\beta+{cos}\alpha}=−\frac{\mathrm{5}}{\mathrm{6}}.\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{5}}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$ \\ $$
