Question Number 88128 by john santu last updated on 08/Apr/20
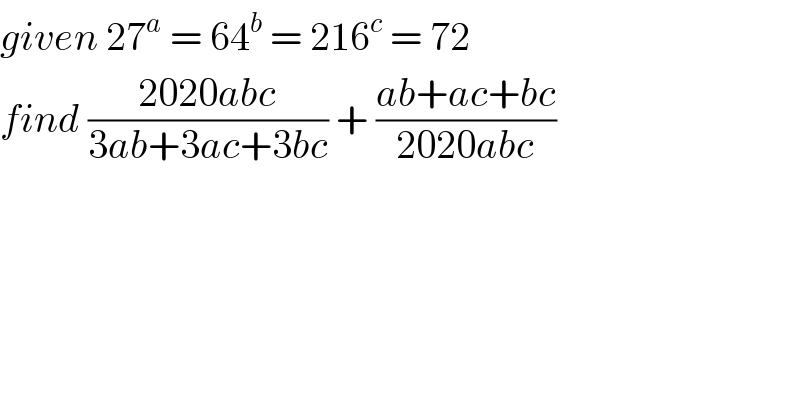
$${given}\:\mathrm{27}^{{a}} \:=\:\mathrm{64}^{{b}} \:=\:\mathrm{216}^{{c}} \:=\:\mathrm{72} \\ $$$${find}\:\frac{\mathrm{2020}{abc}}{\mathrm{3}{ab}+\mathrm{3}{ac}+\mathrm{3}{bc}}\:+\:\frac{{ab}+{ac}+{bc}}{\mathrm{2020}{abc}} \\ $$
Answered by $@ty@m123 last updated on 08/Apr/20
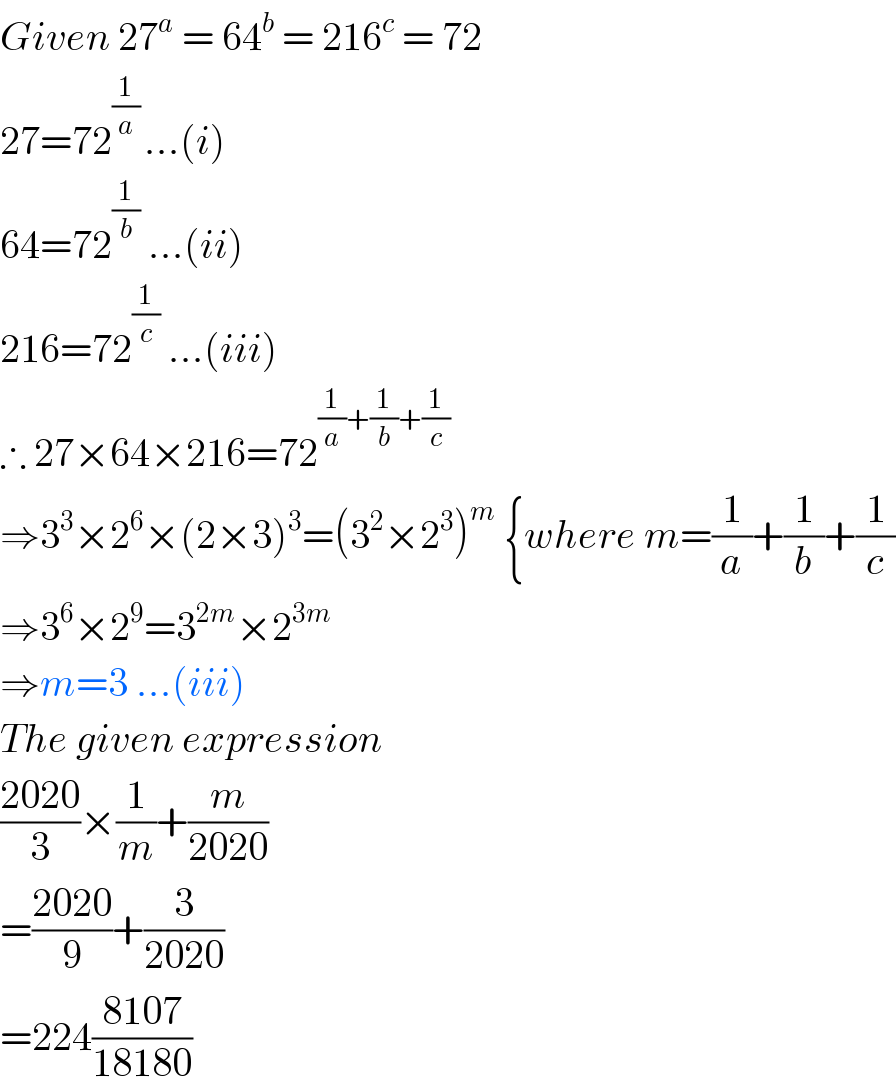
$${Given}\:\mathrm{27}^{{a}} \:=\:\mathrm{64}^{{b}} \:=\:\mathrm{216}^{{c}} \:=\:\mathrm{72} \\ $$$$\mathrm{27}=\mathrm{72}^{\frac{\mathrm{1}}{{a}}\:} …\left({i}\right) \\ $$$$\mathrm{64}=\mathrm{72}^{\frac{\mathrm{1}}{{b}}} \:…\left({ii}\right) \\ $$$$\mathrm{216}=\mathrm{72}^{\frac{\mathrm{1}}{{c}}} \:…\left({iii}\right) \\ $$$$\therefore\:\mathrm{27}×\mathrm{64}×\mathrm{216}=\mathrm{72}^{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{6}} ×\left(\mathrm{2}×\mathrm{3}\right)^{\mathrm{3}} =\left(\mathrm{3}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{3}} \right)^{{m}} \:\left\{{where}\:{m}=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right. \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{6}} ×\mathrm{2}^{\mathrm{9}} =\mathrm{3}^{\mathrm{2}{m}} ×\mathrm{2}^{\mathrm{3}{m}} \\ $$$$\Rightarrow{m}=\mathrm{3}\:…\left({iii}\right) \\ $$$${The}\:{given}\:{expression} \\ $$$$\frac{\mathrm{2020}}{\mathrm{3}}×\frac{\mathrm{1}}{{m}}+\frac{{m}}{\mathrm{2020}} \\ $$$$=\frac{\mathrm{2020}}{\mathrm{9}}+\frac{\mathrm{3}}{\mathrm{2020}} \\ $$$$=\mathrm{224}\frac{\mathrm{8107}}{\mathrm{18180}} \\ $$
Commented by john santu last updated on 08/Apr/20
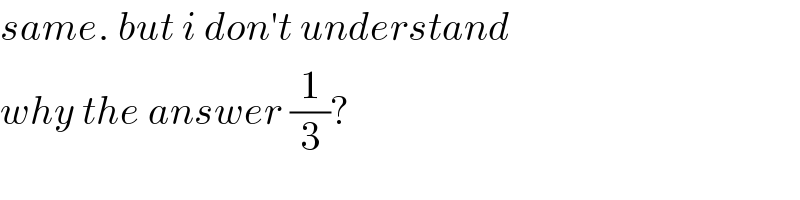
$${same}.\:{but}\:{i}\:{don}'{t}\:{understand}\: \\ $$$${why}\:{the}\:{answer}\:\frac{\mathrm{1}}{\mathrm{3}}? \\ $$
