Given-5x-3y-6-find-min-value-of-x-1-2-y-1-2-

Question Number 99003 by bramlex last updated on 18/Jun/20

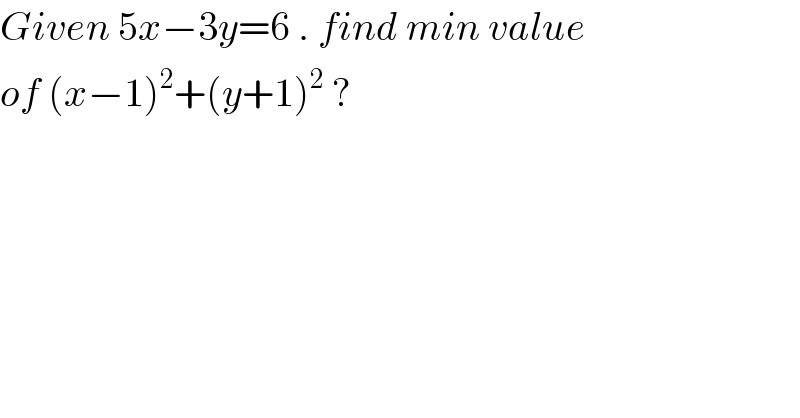
G i v e n 5 x - 3 y = 6 . f i n d m i n v a l u e

o f {(x - 1)}^{2} + {(y + 1)}^{2} ?

Answered by bobhans last updated on 18/Jun/20

let {(x - 1)}^{2} + {(y + 1)}^{2} = R^{2}

\min {{(x - 1)}^{2} + {(y + 1)}^{2}} if 5 x - 3 y = 6 is

tangent line of a circle .

\min value = R^{2} = \frac{∣ 5.1 - 3 . (- 1) - 6 ∣^{2}}{25 + 9}

= \frac{4}{34} = \frac{2}{17}

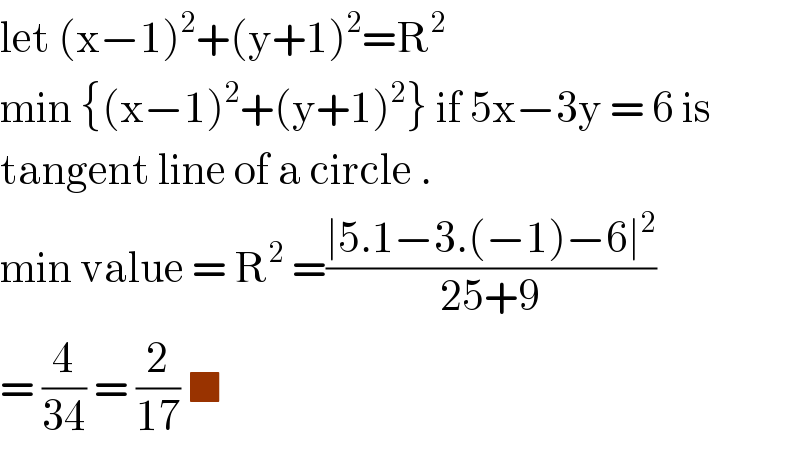
Commented by bramlex last updated on 18/Jun/20

t h a n k y o u

Answered by 1549442205 last updated on 18/Jun/20

5 (x - 1) - 3 (y + 1) = - 2 . ApplyingAM - GM

we get {(- 2)}^{2} ⩽ (5^{2} + {(- 3)}^{2}) [{(x - 1)}^{2} + {(y + 1)}^{2}]

\Rightarrow {(x - 1)}^{2} + {(y + 1)}^{2} ⩾ \frac{4}{34} = \frac{2}{17} . The equality occurs

when {\begin{cases} \frac{5}{x - 1} = \frac{- 3}{y + 1} \\ 5 x - 3 y = 6 \end{cases} \Leftrightarrow {\begin{cases} 3 x + 5 y = - 2 \\ 5 x - 3 y = 6 \end{cases} \Leftrightarrow {\begin{cases} x = \frac{12}{17} \\ y = \frac{- 14}{17} \end{cases}

Hence, S = {(x - 1)}^{2} + {(y + 1)}^{2} has the least value equal to

\frac{2}{34} when {\begin{cases} x = \frac{12}{17} \\ y = \frac{- 14}{17} \end{cases}

Commented by bemath last updated on 18/Jun/20

the last line \frac{2}{34} or \frac{2}{17} or \frac{4}{34} ?

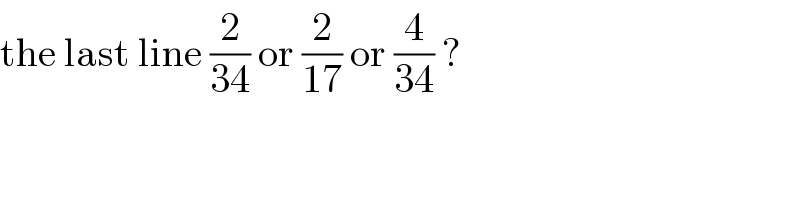
Commented by 1549442205 last updated on 18/Jun/20

Excuse me, thank sir you, I wrote a mistake

it is \frac{2}{17}

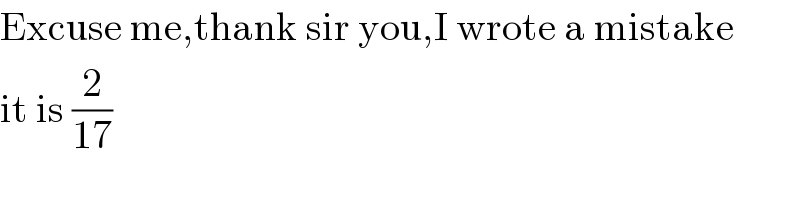
Answered by MJS last updated on 18/Jun/20

why you folks do such complicated things ?

5 x - 3 y = 6 \Rightarrow y = \frac{5}{3} x - 2

{(x - 1)}^{2} + {(y + 1)}^{2} = \frac{34}{9} x^{2} - \frac{16}{3} x + 2

\frac{d}{d x} [\frac{34}{9} x^{2} - \frac{16}{3} x + 2] = 0

\frac{68}{9} x - \frac{16}{3} = 0

x = \frac{12}{17}

\frac{d}{d x} [\frac{68}{9} x - \frac{16}{3}] > 0 \Rightarrow minimum

\frac{34}{9} x^{2} - \frac{16}{3} x + 2 = \frac{2}{17}

Commented by bramlex last updated on 18/Jun/20

t h a n k y o u

Facebook Tweet Pin