Question Number 129949 by bemath last updated on 21/Jan/21
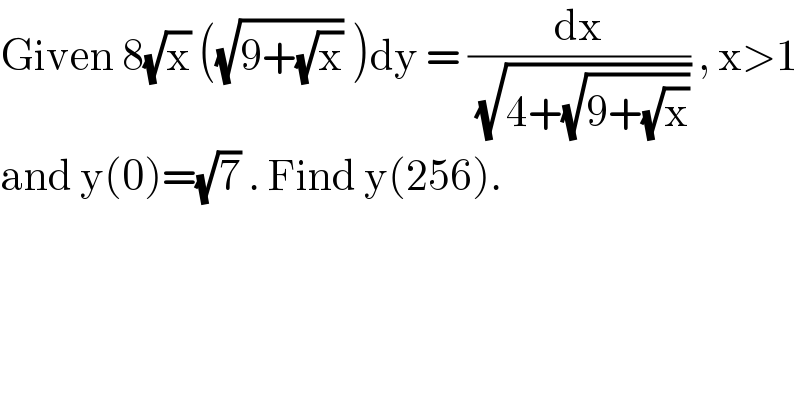
$$\mathrm{Given}\:\mathrm{8}\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}\:\right)\mathrm{dy}\:=\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{4}+\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}}}\:,\:\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{y}\left(\mathrm{0}\right)=\sqrt{\mathrm{7}}\:.\:\mathrm{Find}\:\mathrm{y}\left(\mathrm{256}\right). \\ $$
Answered by liberty last updated on 21/Jan/21
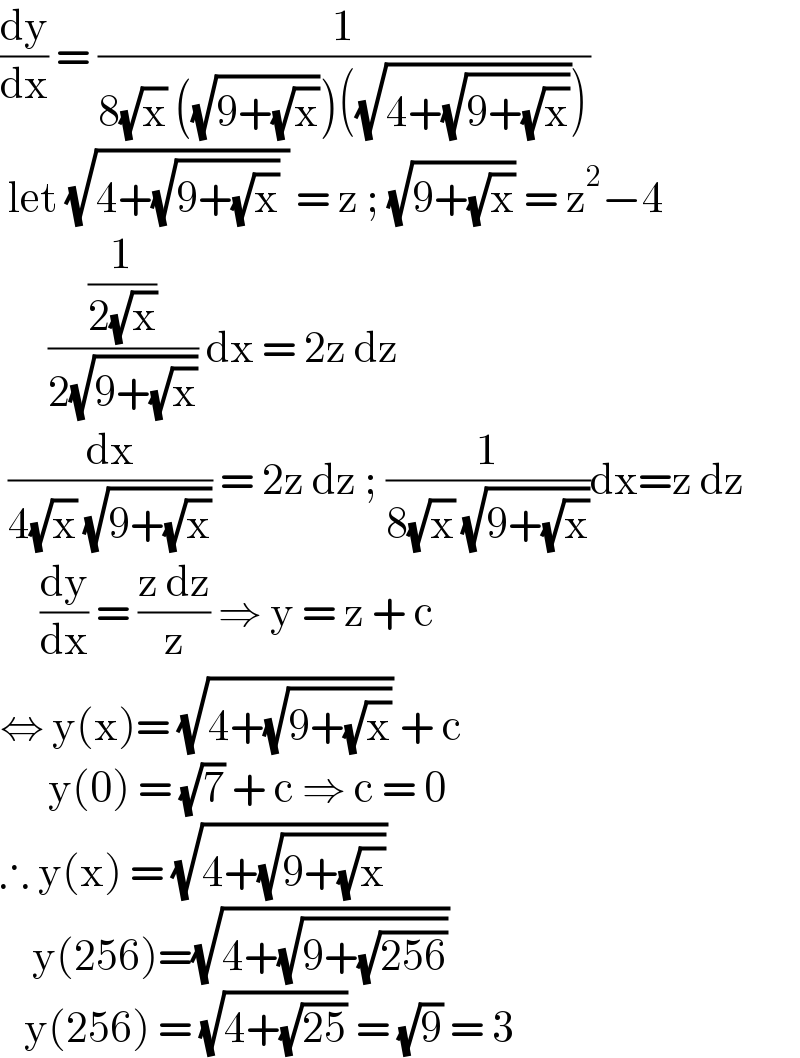
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}\right)\left(\sqrt{\mathrm{4}+\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}}\right)} \\ $$$$\:\mathrm{let}\:\sqrt{\mathrm{4}+\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}\:}\:=\:\mathrm{z}\:;\:\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}\:=\:\mathrm{z}^{\mathrm{2}} −\mathrm{4} \\ $$$$\:\:\:\:\:\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}}{\mathrm{2}\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}}\:\mathrm{dx}\:=\:\mathrm{2z}\:\mathrm{dz}\: \\ $$$$\:\frac{\mathrm{dx}}{\mathrm{4}\sqrt{\mathrm{x}}\:\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}}\:=\:\mathrm{2z}\:\mathrm{dz}\:;\:\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{x}}\:\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}}\mathrm{dx}=\mathrm{z}\:\mathrm{dz} \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{z}\:\mathrm{dz}}{\mathrm{z}}\:\Rightarrow\:\mathrm{y}\:=\:\mathrm{z}\:+\:\mathrm{c} \\ $$$$\Leftrightarrow\:\mathrm{y}\left(\mathrm{x}\right)=\:\sqrt{\mathrm{4}+\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}}\:+\:\mathrm{c} \\ $$$$\:\:\:\:\:\:\mathrm{y}\left(\mathrm{0}\right)\:=\:\sqrt{\mathrm{7}}\:+\:\mathrm{c}\:\Rightarrow\:\mathrm{c}\:=\:\mathrm{0} \\ $$$$\therefore\:\mathrm{y}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{4}+\sqrt{\mathrm{9}+\sqrt{\mathrm{x}}}}\: \\ $$$$\:\:\:\:\mathrm{y}\left(\mathrm{256}\right)=\sqrt{\mathrm{4}+\sqrt{\mathrm{9}+\sqrt{\mathrm{256}}}} \\ $$$$\:\:\:\mathrm{y}\left(\mathrm{256}\right)\:=\:\sqrt{\mathrm{4}+\sqrt{\mathrm{25}}}\:=\:\sqrt{\mathrm{9}}\:=\:\mathrm{3} \\ $$
