Question Number 180014 by cortano1 last updated on 06/Nov/22
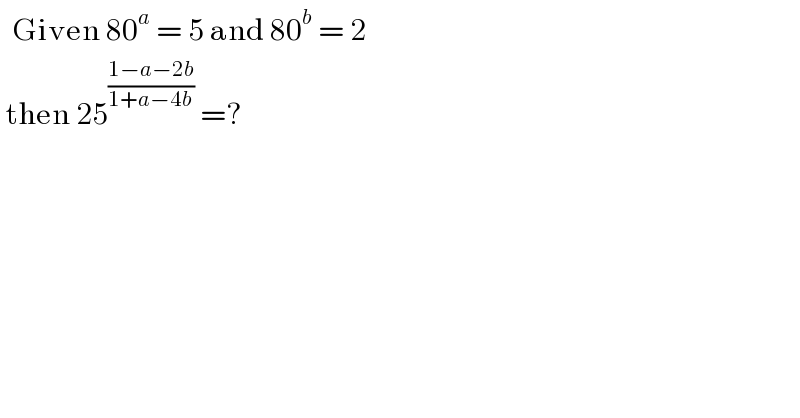
$$\:\:\mathrm{Given}\:\mathrm{80}^{{a}} \:=\:\mathrm{5}\:\mathrm{and}\:\mathrm{80}^{{b}} \:=\:\mathrm{2} \\ $$$$\:\mathrm{then}\:\mathrm{25}^{\frac{\mathrm{1}−{a}−\mathrm{2}{b}}{\mathrm{1}+{a}−\mathrm{4}{b}}} \:=?\: \\ $$
Answered by srikanth2684 last updated on 06/Nov/22
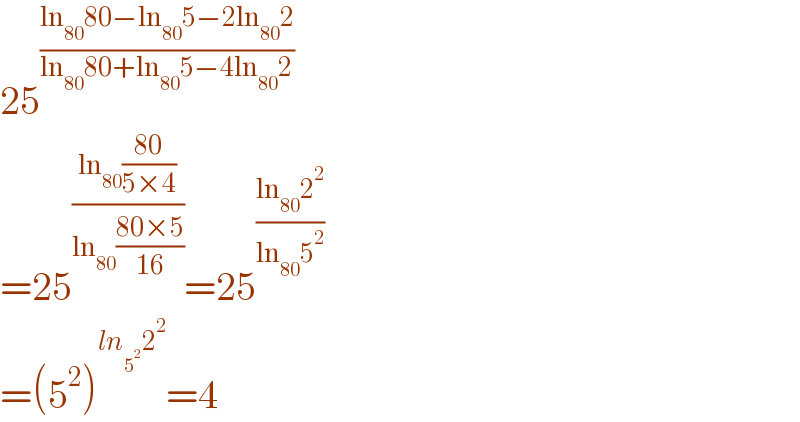
$$\mathrm{25}^{\frac{\mathrm{ln}_{\mathrm{80}} \mathrm{80}−\mathrm{ln}_{\mathrm{80}} \mathrm{5}−\mathrm{2ln}_{\mathrm{80}} \mathrm{2}}{\mathrm{ln}_{\mathrm{80}} \mathrm{80}+\mathrm{ln}_{\mathrm{80}} \mathrm{5}−\mathrm{4ln}_{\mathrm{80}} \mathrm{2}}} \\ $$$$=\mathrm{25}^{\frac{\mathrm{ln}_{\mathrm{80}} \frac{\mathrm{80}}{\mathrm{5}×\mathrm{4}}}{\mathrm{ln}_{\mathrm{80}} \frac{\mathrm{80}×\mathrm{5}}{\mathrm{16}}}} =\mathrm{25}^{\frac{\mathrm{ln}_{\mathrm{80}} \mathrm{2}^{\mathrm{2}} }{\mathrm{ln}_{\mathrm{80}} \mathrm{5}^{\mathrm{2}} }} \\ $$$$=\left(\mathrm{5}^{\mathrm{2}} \right)^{{ln}_{\mathrm{5}^{\mathrm{2}} } \mathrm{2}^{\mathrm{2}} } =\mathrm{4} \\ $$
Commented by cortano1 last updated on 06/Nov/22

$$\mathrm{yes}.\: \\ $$
Answered by a.lgnaoui last updated on 06/Nov/22
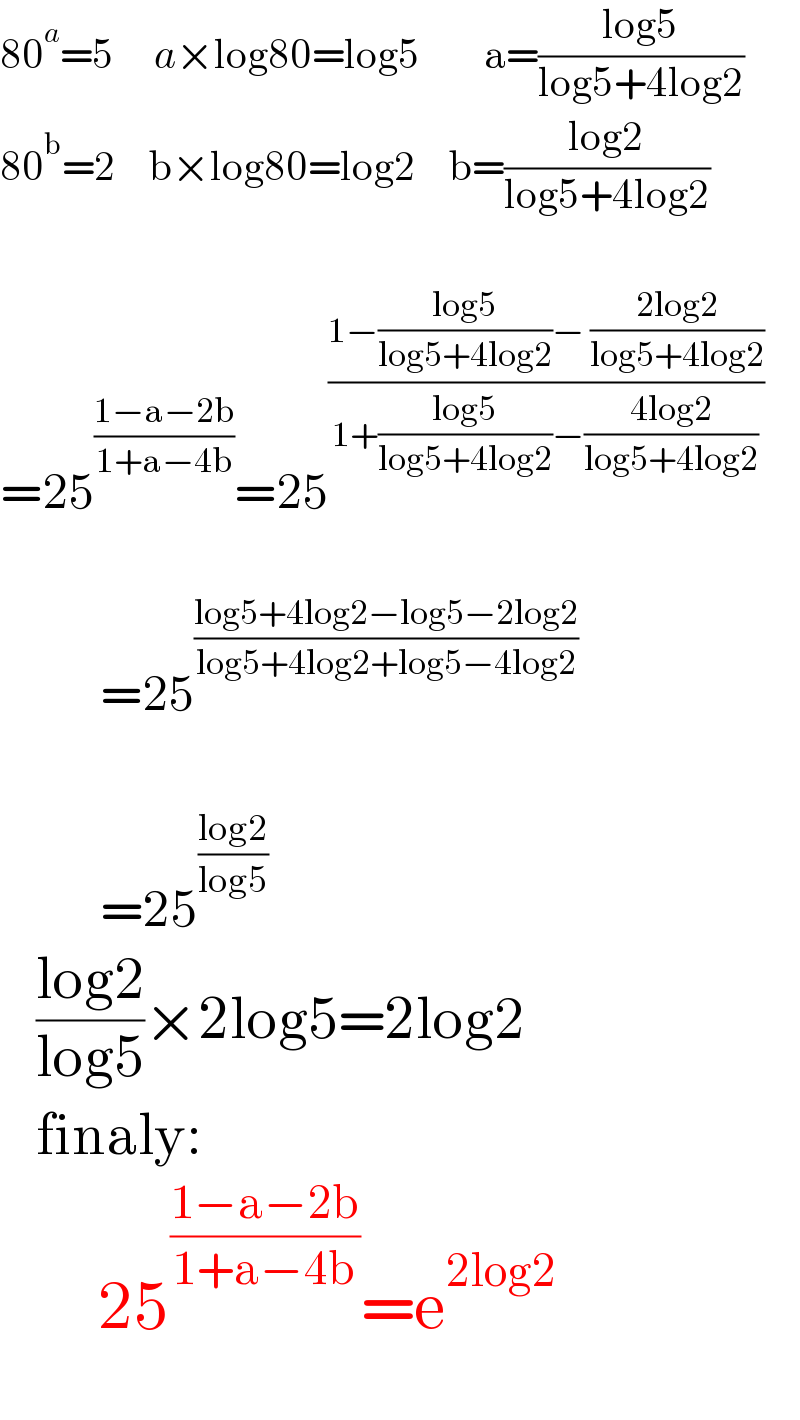
$$\mathrm{80}^{{a}} =\mathrm{5}\:\:\:\:\:{a}×\mathrm{log80}=\mathrm{log5}\:\:\:\:\:\:\:\:\mathrm{a}=\frac{\mathrm{log5}}{\mathrm{log5}+\mathrm{4log2}} \\ $$$$\mathrm{80}^{\mathrm{b}} =\mathrm{2}\:\:\:\:\mathrm{b}×\mathrm{log80}=\mathrm{log2}\:\:\:\:\mathrm{b}=\frac{\mathrm{log2}}{\mathrm{log5}+\mathrm{4log2}} \\ $$$$ \\ $$$$=\mathrm{25}^{\frac{\mathrm{1}−\mathrm{a}−\mathrm{2b}}{\mathrm{1}+\mathrm{a}−\mathrm{4b}}} =\mathrm{25}^{\frac{\mathrm{1}−\frac{\mathrm{log5}}{\mathrm{log5}+\mathrm{4log2}}−\:\frac{\mathrm{2log2}}{\mathrm{log5}+\mathrm{4log2}}}{\mathrm{1}+\frac{\mathrm{log5}}{\mathrm{log5}+\mathrm{4log2}}−\frac{\mathrm{4log2}}{\mathrm{log5}+\mathrm{4log2}}}} \\ $$$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{25}^{\frac{\mathrm{log5}+\mathrm{4log2}−\mathrm{log5}−\mathrm{2log2}}{\mathrm{log5}+\mathrm{4log2}+\mathrm{log5}−\mathrm{4log2}}} \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{25}^{\frac{\mathrm{log2}}{\mathrm{log5}}} \\ $$$$\:\:\:\frac{\mathrm{log2}}{\mathrm{log5}}×\mathrm{2log5}=\mathrm{2log2} \\ $$$$\:\:\:\mathrm{finaly}: \\ $$$$\:\:\:\:\:\:\:\mathrm{25}^{\frac{\mathrm{1}−\mathrm{a}−\mathrm{2b}}{\mathrm{1}+\mathrm{a}−\mathrm{4b}}} =\mathrm{e}^{\mathrm{2log2}} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 06/Nov/22
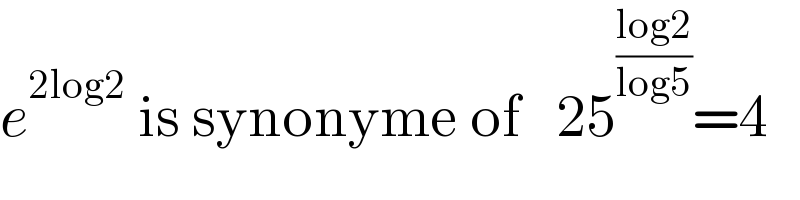
$${e}^{\mathrm{2log2}} \:\mathrm{is}\:\mathrm{synonyme}\:\mathrm{of}\:\:\:\mathrm{25}^{\frac{\mathrm{log2}}{\mathrm{log5}}} =\mathrm{4} \\ $$
Commented by a.lgnaoui last updated on 06/Nov/22
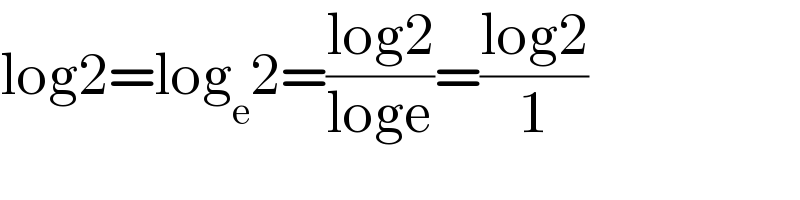
$$\mathrm{log2}=\mathrm{log}_{\mathrm{e}} \mathrm{2}=\frac{\mathrm{log2}}{\mathrm{loge}}=\frac{\mathrm{log2}}{\mathrm{1}} \\ $$
Commented by a.lgnaoui last updated on 06/Nov/22

$${Resultat}:\:\mathrm{4} \\ $$
Commented by cortano1 last updated on 06/Nov/22

$$\left.\mathrm{log}\:\mathrm{2}=\:\mathrm{log}\:_{\mathrm{e}} \left(\mathrm{2}\right)\right)\:? \\ $$
