Question Number 184280 by mr W last updated on 04/Jan/23
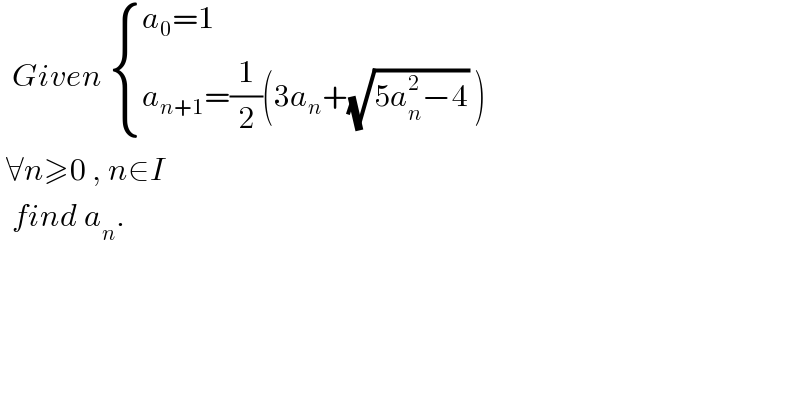
$$\:\:{Given}\:\begin{cases}{{a}_{\mathrm{0}} =\mathrm{1}}\\{{a}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{a}_{{n}} +\sqrt{\mathrm{5}{a}_{{n}} ^{\mathrm{2}} −\mathrm{4}}\:\right)}\end{cases} \\ $$$$\:\forall{n}\geqslant\mathrm{0}\:,\:{n}\in{I}\: \\ $$$$\:\:{find}\:{a}_{{n}} . \\ $$
Commented by mr W last updated on 04/Jan/23
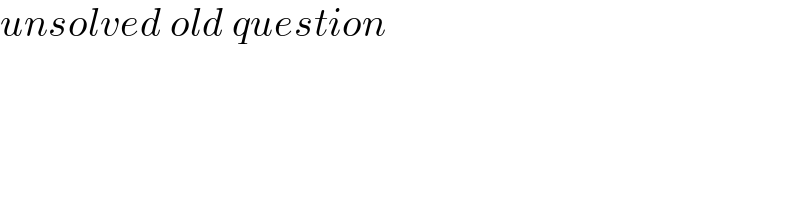
$${unsolved}\:{old}\:{question} \\ $$
Commented by mr W last updated on 04/Jan/23
![i found finally a solution: a_n =(2/( (√5))) cosh [(2n+1) cosh^(−1) ((√5)/2) ] which delivers: a_0 =1 a_1 =2 a_2 =5 a_3 =13 a_4 =34 a_5 =89 ...](https://www.tinkutara.com/question/Q184283.png)
$${i}\:{found}\:{finally}\:{a}\:{solution}: \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left[\left(\mathrm{2}{n}+\mathrm{1}\right)\:\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\right] \\ $$$${which}\:{delivers}: \\ $$$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${a}_{\mathrm{1}} =\mathrm{2} \\ $$$${a}_{\mathrm{2}} =\mathrm{5} \\ $$$${a}_{\mathrm{3}} =\mathrm{13} \\ $$$${a}_{\mathrm{4}} =\mathrm{34} \\ $$$${a}_{\mathrm{5}} =\mathrm{89} \\ $$$$… \\ $$
Commented by mr W last updated on 04/Jan/23
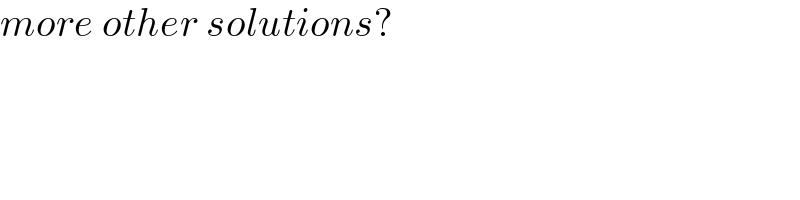
$${more}\:{other}\:{solutions}? \\ $$
Commented by SEKRET last updated on 04/Jan/23

$$\:\:\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} =\:\frac{\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}−\mathrm{1}} \:+\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}+\mathrm{1}} }{\mathrm{3}} \\ $$
Commented by SEKRET last updated on 04/Jan/23

$$\:\:\boldsymbol{\mathrm{a}}_{\mathrm{0}} =\mathrm{1} \\ $$$$\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{1}} =\:\mathrm{2}\centerdot\mathrm{1}+\mathrm{0} \\ $$$$\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{2}} =\:\mathrm{2}+\left(\mathrm{2}+\mathrm{1}\right) \\ $$$$\:\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{3}} =\:\mathrm{5}+\left(\mathrm{5}+\mathrm{2}+\mathrm{1}\right) \\ $$$$\:\boldsymbol{\mathrm{a}}_{\mathrm{4}} =\:\mathrm{13}+\left(\mathrm{13}+\mathrm{5}+\mathrm{2}+\mathrm{1}\right) \\ $$$$\:\:\boldsymbol{\mathrm{a}}_{\mathrm{5}} =\:\mathrm{34}+\:\left(\mathrm{34}+\mathrm{13}+\mathrm{5}+\mathrm{2}+\mathrm{1}\right) \\ $$$$……….. \\ $$$$\:\:\:\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} =\:\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}−\mathrm{1}} +\underset{\boldsymbol{\mathrm{k}}=\mathrm{0}} {\overset{\boldsymbol{\mathrm{n}}−\mathrm{1}} {\sum}}\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{k}}} \\ $$
Commented by SEKRET last updated on 04/Jan/23
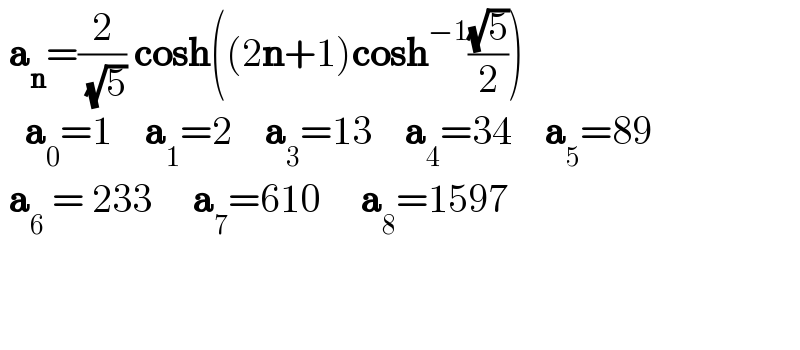
$$\:\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\boldsymbol{\mathrm{cosh}}\left(\left(\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}\right)\boldsymbol{\mathrm{cosh}}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{0}} =\mathrm{1}\:\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{1}} =\mathrm{2}\:\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{3}} =\mathrm{13}\:\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{4}} =\mathrm{34}\:\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{5}} =\mathrm{89} \\ $$$$\:\boldsymbol{\mathrm{a}}_{\mathrm{6}} \:=\:\mathrm{233}\:\:\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{7}} =\mathrm{610}\:\:\:\:\:\boldsymbol{\mathrm{a}}_{\mathrm{8}} =\mathrm{1597}\:\: \\ $$$$\:\:\: \\ $$$$ \\ $$
Commented by SEKRET last updated on 04/Jan/23
$$\:\:\boldsymbol{\mathrm{how}}\:\:\boldsymbol{\mathrm{did}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{it}} \\ $$
Commented by mr W last updated on 04/Jan/23

$${thanks}! \\ $$$${but}\:{the}\:{question}\:{asks}\:{for}\:{a}_{{n}} \:{in} \\ $$$${explicit}\:{form}.\:{recursive}\:{form}\:{is} \\ $$$${already}\:{given}\:{in}\:{the}\:{question}. \\ $$
Commented by SEKRET last updated on 04/Jan/23

$$\boldsymbol{\mathrm{right}} \\ $$
Commented by Frix last updated on 04/Jan/23

$$\mathrm{It}'\mathrm{s}\:\mathrm{each}\:\mathrm{2nd}\:\mathrm{Fibonacci}−\mathrm{Number}\:\Rightarrow \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} \right) \\ $$
Commented by mr W last updated on 04/Jan/23
$${how}\:{did}\:{you}\:{get}\:{this}? \\ $$
Commented by manxsol last updated on 05/Jan/23

$${tru}\bar {{e}},\:\:\:{good}\:{observation}\:{Sr}.{Frix} \\ $$$$\begin{array}{|c|c|c|}{{n}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{6}}&\hline{\mathrm{7}}&\hline{\mathrm{8}}&\hline{\mathrm{9}}&\hline{\mathrm{10}}\\{{f}_{{n}} }&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{5}}&\hline{\mathrm{8}}&\hline{\mathrm{13}}&\hline{\mathrm{21}}&\hline{\mathrm{34}}&\hline{\mathrm{55}}&\hline{\mathrm{89}}\\{{a}_{{n}} }&\hline{}&\hline{\mathrm{2}}&\hline{}&\hline{\mathrm{5}}&\hline{}&\hline{\mathrm{13}}&\hline{}&\hline{\mathrm{34}}&\hline{}&\hline{\mathrm{89}}\\\hline\end{array} \\ $$$${a}_{{n}} ={f}_{\mathrm{2}{n}−\mathrm{2}} \:\:\:{a}_{\mathrm{1}} =\mathrm{1} \\ $$$${this}\:{solution}\:{is}\:{valid}? \\ $$$$\:\:{a}_{{n}} ={f}_{\mathrm{2}{n}−\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 05/Jan/23

$${so}\:{far}\:{as}\:{it}\:{is}\:{not}\:{deviated}\:{from}\:{the} \\ $$$${given}\:{equation}\:{a}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{a}_{{n}} +\sqrt{\mathrm{5}{a}_{{n}} ^{\mathrm{2}} −\mathrm{4}}\right), \\ $$$${i}\:{don}'{t}\:{think}\:{it}\:{is}\:{mathematically} \\ $$$${strict},\:{even}\:{though}\:{it}\:{is}\:{correct}. \\ $$$${the}\:{question}\:{is}\:{not}: \\ $$$${given}:\:\mathrm{1},\mathrm{2},\mathrm{5},\mathrm{13},\mathrm{34},…\:{find}\:{a}_{{n}} =?. \\ $$$${and}\:{even}\:{so},\:{there}\:{are}\:{infinite} \\ $$$${solutions}\:{for}\:{a}_{{n}} \:{as}\:{we}\:{know}. \\ $$
Answered by mr W last updated on 05/Jan/23
![a_(n+1) =(1/2)(3a_n +(√(5a_n ^2 −4))) 2a_(n+1) −3a_n =(√(5a_n ^2 −4)) a_(n+1) ^2 −3a_(n+1) a_n +a_n ^2 +1=0 (a_(n+1) −a_n )^2 +1=a_(n+1) a_n let a_(n+1) +a_n =u a_(n+1) −a_n =v ⇒u^2 −5v^2 =4 ((u/2))^2 −((((√5)v)/2))^2 =1 cosh^2 x_n −sinh^2 x_n =1 (u/2)=cosh x_n ⇒u=2 cosh x_n (((√5)v)/2)=sinh x_n ⇒v=((2 sinh x_n )/( (√5))) a_n =(1/2)(u−v)=cosh x_n −((sinh x_n )/( (√5))) a_n =(2/( (√5)))(((√5)/2) cosh x_n −(1/2) sinh x_n ) a_n =(2/( (√5)))(cosh x_n cosh α−sinh x_n sinh α)=kcosh (x_n −α) a_n =(2/( (√5))) cosh (x_n −α) with α=cosh^(−1) ((√5)/2) a_(n+1) =(1/2)(u+v)=cosh x_n +((sinh x_n )/( (√5))) a_(n+1) =(2/( (√5)))(((√5)/2) cosh x_n +(1/2) sinh x_n ) a_(n+1) =(2/( (√5))) (cosh x_n cosh α+sinh x_n sinh α) a_(n+1) =(2/( (√5))) cosh (x_n +α) on the other side: a_(n+1) =(2/( (√5))) cosh (x_(n+1) −α) ⇒cosh (x_(n+1) −α)=cosh (x_n +α) ⇒x_(n+1) −α=x_n +α ⇒x_(n+1) =x_n +2α ← A.P. with c.d. =2α ⇒x_n =x_0 +2nα a_n =(2/( (√5))) cosh (x_0 +2nα−α) ⇒a_n =(2/( (√5))) cosh [x_0 +(2n−1) cosh^(−1) ((√5)/2)] a_0 =(2/( (√5))) cosh (x_0 −cosh^(−1) ((√5)/2))=1 ⇒x_0 =2 cosh^(−1) ((√5)/2) ⇒a_n =(2/( (√5))) cosh [(2n+1)cosh^(−1) ((√5)/2)] additionally: cosh^(−1) ((√5)/2)=ln (((√5)/2)+(√((((√5)/2))^2 −1)))=ln (((√5)+1)/2) (2n+1)cosh^(−1) ((√5)/2)=ln ((((√5)+1)/2))^((2n+1)) e^(−(2n+1)cosh^(−1) ((√5)/2)) =((((√5)+1)/2))^(−(2n+1)) =((((√5)−1)/2))^((2n+1)) a_n =(2/( (√5))) cosh [(2n+1)cosh^(−1) ((√5)/2)] a_n =(1/( (√5)))[e^((2n+1)cosh^(−1) ((√5)/2)) +e^(−(2n+1)cosh^(−1) ((√5)/2)) ] ⇒a_n =(1/( (√5)))[((((√5)+1)/2))^((2n+1)) +((((√5)−1)/2))^((2n+1)) ]](https://www.tinkutara.com/question/Q184294.png)
$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{a}_{{n}} +\sqrt{\mathrm{5}{a}_{{n}} ^{\mathrm{2}} −\mathrm{4}}\right) \\ $$$$\mathrm{2}{a}_{{n}+\mathrm{1}} −\mathrm{3}{a}_{{n}} =\sqrt{\mathrm{5}{a}_{{n}} ^{\mathrm{2}} −\mathrm{4}} \\ $$$${a}_{{n}+\mathrm{1}} ^{\mathrm{2}} −\mathrm{3}{a}_{{n}+\mathrm{1}} {a}_{{n}} +{a}_{{n}} ^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\left({a}_{{n}+\mathrm{1}} −{a}_{{n}} \right)^{\mathrm{2}} +\mathrm{1}={a}_{{n}+\mathrm{1}} {a}_{{n}} \\ $$$${let}\: \\ $$$${a}_{{n}+\mathrm{1}} +{a}_{{n}} ={u} \\ $$$${a}_{{n}+\mathrm{1}} −{a}_{{n}} ={v} \\ $$$$\Rightarrow{u}^{\mathrm{2}} −\mathrm{5}{v}^{\mathrm{2}} =\mathrm{4} \\ $$$$\left(\frac{{u}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{5}}{v}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{cosh}^{\mathrm{2}} \:{x}_{{n}} −\mathrm{sinh}^{\mathrm{2}} \:{x}_{{n}} =\mathrm{1} \\ $$$$\frac{{u}}{\mathrm{2}}=\mathrm{cosh}\:{x}_{{n}} \:\:\Rightarrow{u}=\mathrm{2}\:\mathrm{cosh}\:{x}_{{n}} \\ $$$$\frac{\sqrt{\mathrm{5}}{v}}{\mathrm{2}}=\mathrm{sinh}\:{x}_{{n}} \:\Rightarrow{v}=\frac{\mathrm{2}\:\mathrm{sinh}\:{x}_{{n}} }{\:\sqrt{\mathrm{5}}} \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left({u}−{v}\right)=\mathrm{cosh}\:{x}_{{n}} −\frac{\mathrm{sinh}\:{x}_{{n}} }{\:\sqrt{\mathrm{5}}} \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{cosh}\:{x}_{{n}} −\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sinh}\:{x}_{{n}} \right) \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left(\mathrm{cosh}\:{x}_{{n}} \:\mathrm{cosh}\:\alpha−\mathrm{sinh}\:{x}_{{n}} \:\mathrm{sinh}\:\alpha\right)={k}\mathrm{cosh}\:\left({x}_{{n}} −\alpha\right) \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left({x}_{{n}} −\alpha\right)\:{with}\:\alpha=\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left({u}+{v}\right)=\mathrm{cosh}\:{x}_{{n}} +\frac{\mathrm{sinh}\:{x}_{{n}} }{\:\sqrt{\mathrm{5}}} \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{cosh}\:{x}_{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sinh}\:{x}_{{n}} \right) \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\left(\mathrm{cosh}\:{x}_{{n}} \:\mathrm{cosh}\:\alpha+\mathrm{sinh}\:{x}_{{n}} \:\mathrm{sinh}\:\alpha\right) \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left({x}_{{n}} +\alpha\right) \\ $$$${on}\:{the}\:{other}\:{side}: \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left({x}_{{n}+\mathrm{1}} −\alpha\right) \\ $$$$\Rightarrow\mathrm{cosh}\:\left({x}_{{n}+\mathrm{1}} −\alpha\right)=\mathrm{cosh}\:\left({x}_{{n}} +\alpha\right) \\ $$$$\Rightarrow{x}_{{n}+\mathrm{1}} −\alpha={x}_{{n}} +\alpha \\ $$$$\Rightarrow{x}_{{n}+\mathrm{1}} ={x}_{{n}} +\mathrm{2}\alpha\:\:\leftarrow\:{A}.{P}.\:{with}\:{c}.{d}.\:=\mathrm{2}\alpha \\ $$$$\Rightarrow{x}_{{n}} ={x}_{\mathrm{0}} +\mathrm{2}{n}\alpha \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left({x}_{\mathrm{0}} +\mathrm{2}{n}\alpha−\alpha\right) \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left[{x}_{\mathrm{0}} +\left(\mathrm{2}{n}−\mathrm{1}\right)\:\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right] \\ $$$${a}_{\mathrm{0}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left({x}_{\mathrm{0}} −\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\mathrm{1} \\ $$$$\Rightarrow{x}_{\mathrm{0}} =\mathrm{2}\:\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left[\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right] \\ $$$$ \\ $$$${additionally}: \\ $$$$\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}=\mathrm{ln}\:\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\sqrt{\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}}\right)=\mathrm{ln}\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}=\mathrm{ln}\:\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)^{\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$${e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}} =\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)^{−\left(\mathrm{2}{n}+\mathrm{1}\right)} =\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)^{\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\mathrm{cosh}\:\left[\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right] \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[{e}^{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}} +{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}} \right] \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)^{\left(\mathrm{2}{n}+\mathrm{1}\right)} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)^{\left(\mathrm{2}{n}+\mathrm{1}\right)} \right] \\ $$
Commented by SEKRET last updated on 05/Jan/23
$$\:\:\boldsymbol{\mathrm{beatiful}}\:\boldsymbol{\mathrm{solution}} \\ $$
Commented by Frix last updated on 05/Jan/23
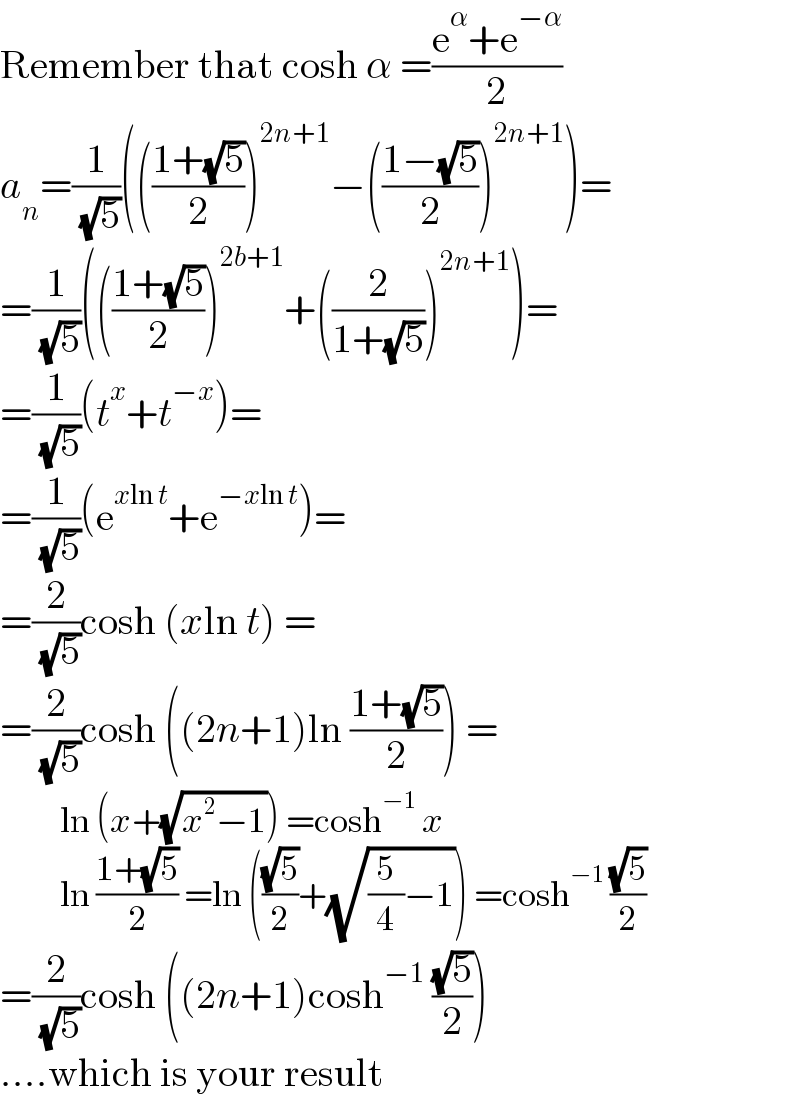
$$\mathrm{Remember}\:\mathrm{that}\:\mathrm{cosh}\:\alpha\:=\frac{\mathrm{e}^{\alpha} +\mathrm{e}^{−\alpha} }{\mathrm{2}} \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} \right)= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}{b}+\mathrm{1}} +\left(\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{5}}}\right)^{\mathrm{2}{n}+\mathrm{1}} \right)= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left({t}^{{x}} +{t}^{−{x}} \right)= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\mathrm{e}^{{x}\mathrm{ln}\:{t}} +\mathrm{e}^{−{x}\mathrm{ln}\:{t}} \right)= \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\mathrm{cosh}\:\left({x}\mathrm{ln}\:{t}\right)\:= \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\mathrm{cosh}\:\left(\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:=\mathrm{cosh}^{−\mathrm{1}} \:{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:=\mathrm{ln}\:\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\sqrt{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{1}}\right)\:=\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\mathrm{cosh}\:\left(\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$….\mathrm{which}\:\mathrm{is}\:\mathrm{your}\:\mathrm{result} \\ $$
Commented by mr W last updated on 05/Jan/23
![thanks sir! i′ve also added the deduction to a_n =(1/( (√5)))[((((√5)+1)/2))^((2n+1)) +((((√5)−1)/2))^((2n+1)) ]. see above.](https://www.tinkutara.com/question/Q184323.png)
$${thanks}\:{sir}! \\ $$$${i}'{ve}\:{also}\:{added}\:{the}\:{deduction}\:{to} \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)^{\left(\mathrm{2}{n}+\mathrm{1}\right)} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)^{\left(\mathrm{2}{n}+\mathrm{1}\right)} \right]. \\ $$$${see}\:{above}. \\ $$
