given-a-1-2-a-2-3-and-a-n-2-a-n-1-a-n-2-find-a-n-

Question Number 81446 by john santu last updated on 13/Feb/20

given a_{1} = 2, a_{2} = 3 and

a_{n + 2} = a_{n + 1} + \frac{a_{n}}{2}

find a_{n} = ?

Commented by mr W last updated on 13/Feb/20

q^{2} - q - \frac{1}{2} = 0

q = \frac{1 \pm \sqrt{3}}{2}

a_{n} = A {(\frac{1 + \sqrt{3}}{2})}^{n} + B {(\frac{1 - \sqrt{3}}{2})}^{n}

a_{1} = A (\frac{1 + \sqrt{3}}{2}) + B (\frac{1 - \sqrt{3}}{2}) = 2

a_{2} = A {(\frac{1 + \sqrt{3}}{2})}^{2} + B {(\frac{1 - \sqrt{3}}{2})}^{2} = 3

\Rightarrow A + B = 2

\Rightarrow A - B = \frac{2 \sqrt{3}}{3}

\Rightarrow A = \frac{3 + \sqrt{3}}{3}

\Rightarrow B = \frac{3 - \sqrt{3}}{3}

\Rightarrow a_{n} = (\frac{3 + \sqrt{3}}{3}) {(\frac{1 + \sqrt{3}}{2})}^{n} + (\frac{3 - \sqrt{3}}{3}) {(\frac{1 - \sqrt{3}}{2})}^{n}

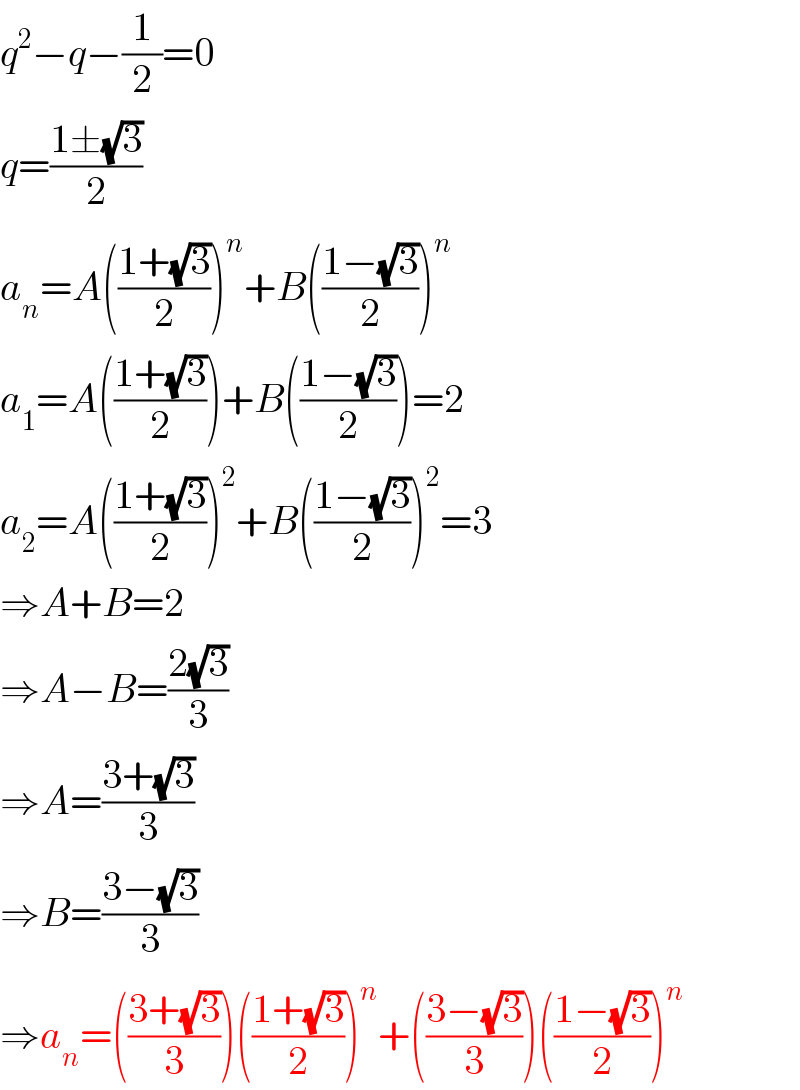
Commented by behi83417@gmail.com last updated on 13/Feb/20

a_{n} = \frac{1}{\sqrt{3}} [{(\frac{1 + \sqrt{3}}{2})}^{n + 1} - {(\frac{1 - \sqrt{3}}{2})}^{n + 1}]

Commented by jagoll last updated on 13/Feb/20

from a_{n} = (\frac{3 + \sqrt{3}}{3}) {(\frac{1 + \sqrt{3}}{2})}^{n} + (\frac{3 - \sqrt{3}}{3}) {(\frac{1 - \sqrt{3}}{2})}^{n}

a_{1} = (\frac{3 + \sqrt{3}}{3}) (\frac{1 + \sqrt{3}}{2}) + (\frac{3 - \sqrt{3}}{3}) (\frac{1 - \sqrt{3}}{2})

= \frac{6 + 4 \sqrt{3} + 6 - 4 \sqrt{3}}{6} = \frac{12}{6} = 2

amazing sir

Commented by john santu last updated on 13/Feb/20

in generally

if \Rightarrow {2 a}_{n + 2} = {3 a}_{n + 1} - \frac{a_{n}}{3}

\Rightarrow {2 q}^{2} - 3 q + \frac{1}{3} = 0

{6 q}^{2} - 9 q + 1 = 0

q = \frac{9 \pm \sqrt{81 - 24}}{12} = \frac{9 \pm \sqrt{57}}{12}

a_{n} = A {(\frac{9 - \sqrt{57}}{12})}^{n} + B {(\frac{9 + \sqrt{57}}{12})}^{n}

Commented by jagoll last updated on 13/Feb/20

thank you mister W . i have the

same problem with this kind .

Facebook Tweet Pin