Given-a-function-f-x-3-f-x-for-x-R-If-3-6-f-x-dx-6-then-3-9-f-x-dx-

Question Number 109101 by bemath last updated on 21/Aug/20

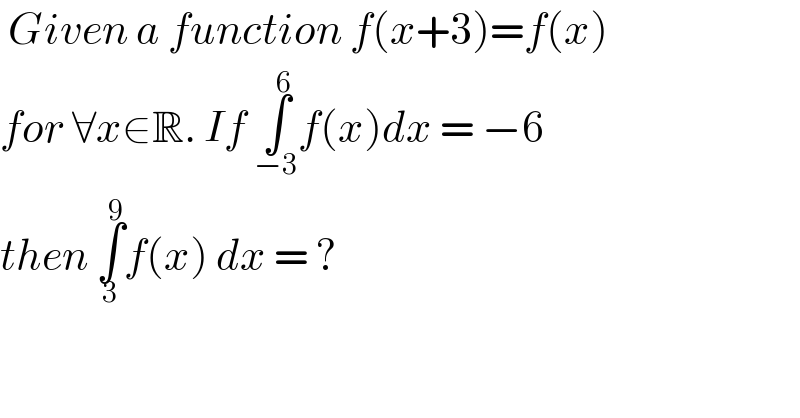
$$\:{Given}\:{a}\:{function}\:{f}\left({x}+\mathrm{3}\right)={f}\left({x}\right) \\ $$$${for}\:\forall{x}\in\mathbb{R}.\:{If}\:\underset{−\mathrm{3}} {\overset{\mathrm{6}} {\int}}{f}\left({x}\right){dx}\:=\:−\mathrm{6}\: \\ $$$${then}\:\underset{\mathrm{3}} {\overset{\mathrm{9}} {\int}}{f}\left({x}\right)\:{dx}\:=\:? \\ $$

Answered by bemath last updated on 21/Aug/20

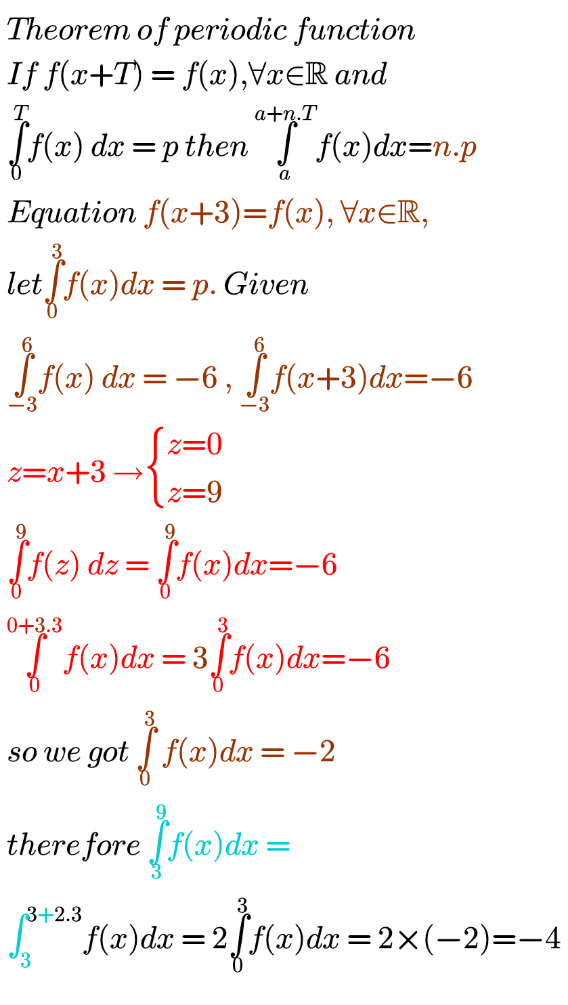
Answered by john santu last updated on 21/Aug/20

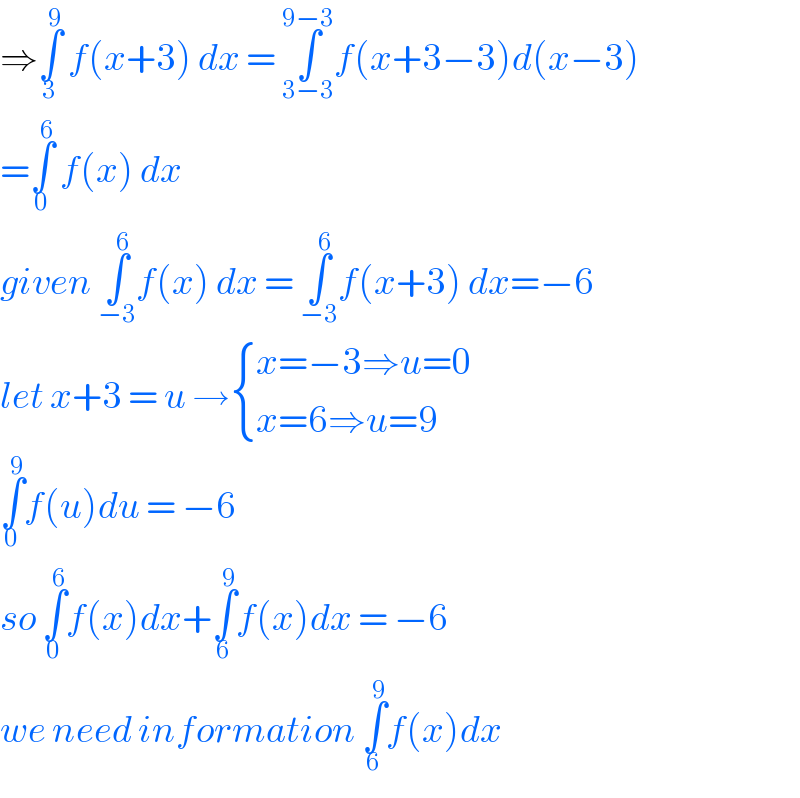
⇒∫_3 ^9 f(x+3) dx = ∫_(3−3) ^(9−3) f(x+3−3)d(x−3) =∫_0 ^6 f(x) dx given ∫_(−3) ^6 f(x) dx = ∫_(−3) ^6 f(x+3) dx=−6 let x+3 = u → { ((x=−3⇒u=0)),((x=6⇒u=9)) :} ∫_0 ^9 f(u)du = −6 so ∫_0 ^6 f(x)dx+∫_6 ^9 f(x)dx = −6 we need information ∫_6 ^9 f(x)dx

$$\Rightarrow\underset{\mathrm{3}} {\overset{\mathrm{9}} {\int}}\:{f}\left({x}+\mathrm{3}\right)\:{dx}\:=\:\underset{\mathrm{3}−\mathrm{3}} {\overset{\mathrm{9}−\mathrm{3}} {\int}}{f}\left({x}+\mathrm{3}−\mathrm{3}\right){d}\left({x}−\mathrm{3}\right) \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{6}} {\int}}\:{f}\left({x}\right)\:{dx}\: \\ $$$${given}\:\underset{−\mathrm{3}} {\overset{\mathrm{6}} {\int}}{f}\left({x}\right)\:{dx}\:=\:\underset{−\mathrm{3}} {\overset{\mathrm{6}} {\int}}{f}\left({x}+\mathrm{3}\right)\:{dx}=−\mathrm{6} \\ $$$${let}\:{x}+\mathrm{3}\:=\:{u}\:\rightarrow\begin{cases}{{x}=−\mathrm{3}\Rightarrow{u}=\mathrm{0}}\\{{x}=\mathrm{6}\Rightarrow{u}=\mathrm{9}}\end{cases} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{9}} {\int}}{f}\left({u}\right){du}\:=\:−\mathrm{6} \\ $$$${so}\:\underset{\mathrm{0}} {\overset{\mathrm{6}} {\int}}{f}\left({x}\right){dx}+\underset{\mathrm{6}} {\overset{\mathrm{9}} {\int}}{f}\left({x}\right){dx}\:=\:−\mathrm{6} \\ $$$${we}\:{need}\:{information}\:\underset{\mathrm{6}} {\overset{\mathrm{9}} {\int}}{f}\left({x}\right){dx} \\ $$

Answered by mr W last updated on 21/Aug/20

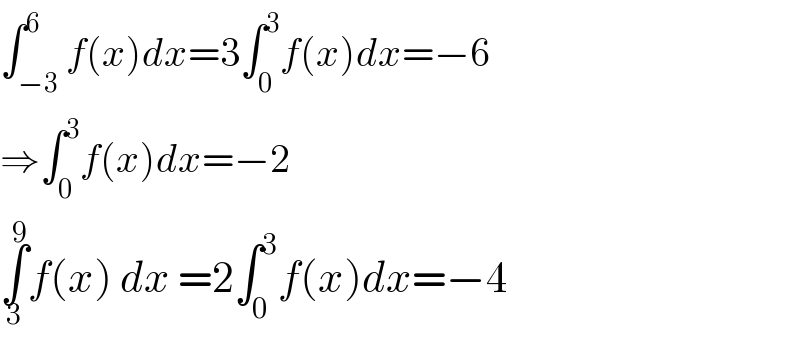
∫_(−3) ^6 f(x)dx=3∫_0 ^3 f(x)dx=−6 ⇒∫_0 ^3 f(x)dx=−2 ∫_3 ^9 f(x) dx =2∫_0 ^3 f(x)dx=−4

$$\int_{−\mathrm{3}} ^{\mathrm{6}} {f}\left({x}\right){dx}=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{3}} {f}\left({x}\right){dx}=−\mathrm{6} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{3}} {f}\left({x}\right){dx}=−\mathrm{2} \\ $$$$\underset{\mathrm{3}} {\overset{\mathrm{9}} {\int}}{f}\left({x}\right)\:{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{3}} {f}\left({x}\right){dx}=−\mathrm{4} \\ $$

Commented by bemath last updated on 21/Aug/20

$${yes}…{hoorraayy} \\ $$

Facebook Tweet Pin

Given-a-function-f-x-3-f-x-for-x-R-If-3-6-f-x-dx-6-then-3-9-f-x-dx-

Leave a Reply Cancel reply