Question Number 118231 by bemath last updated on 16/Oct/20
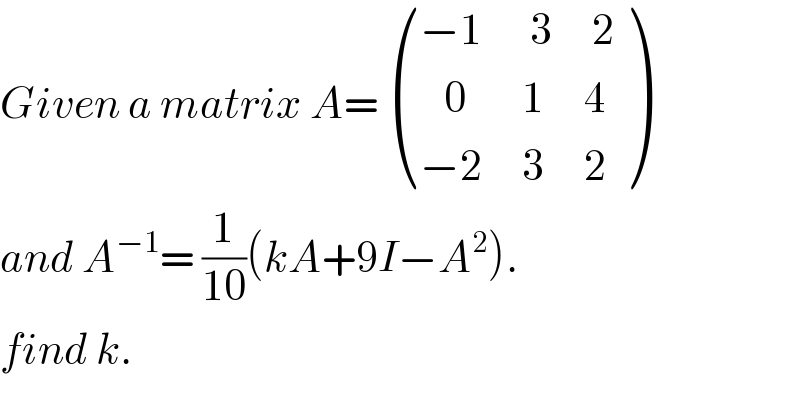
$${Given}\:{a}\:{matrix}\:{A}=\:\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{2}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{4}}\\{−\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{2}}\end{pmatrix} \\ $$$${and}\:{A}^{−\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{10}}\left({kA}+\mathrm{9}{I}−{A}^{\mathrm{2}} \right). \\ $$$${find}\:{k}. \\ $$
Answered by bobhans last updated on 16/Oct/20
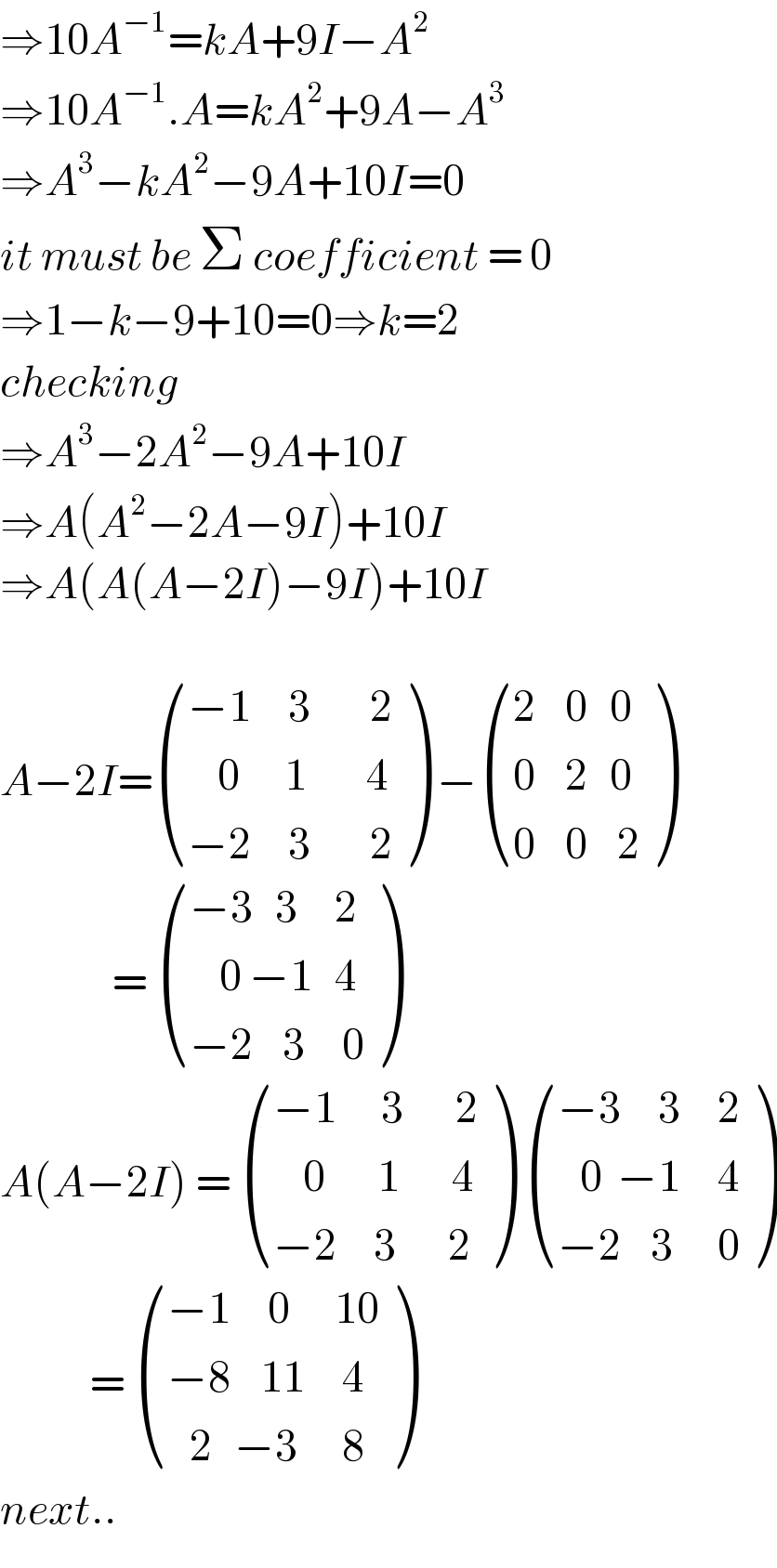
$$\Rightarrow\mathrm{10}{A}^{−\mathrm{1}} ={kA}+\mathrm{9}{I}−{A}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{10}{A}^{−\mathrm{1}} .{A}={kA}^{\mathrm{2}} +\mathrm{9}{A}−{A}^{\mathrm{3}} \\ $$$$\Rightarrow{A}^{\mathrm{3}} −{kA}^{\mathrm{2}} −\mathrm{9}{A}+\mathrm{10}{I}=\mathrm{0} \\ $$$${it}\:{must}\:{be}\:\Sigma\:{coefficient}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−{k}−\mathrm{9}+\mathrm{10}=\mathrm{0}\Rightarrow{k}=\mathrm{2} \\ $$$${checking} \\ $$$$\Rightarrow{A}^{\mathrm{3}} −\mathrm{2}{A}^{\mathrm{2}} −\mathrm{9}{A}+\mathrm{10}{I} \\ $$$$\Rightarrow{A}\left({A}^{\mathrm{2}} −\mathrm{2}{A}−\mathrm{9}{I}\right)+\mathrm{10}{I} \\ $$$$\Rightarrow{A}\left({A}\left({A}−\mathrm{2}{I}\right)−\mathrm{9}{I}\right)+\mathrm{10}{I} \\ $$$$ \\ $$$${A}−\mathrm{2}{I}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{2}}\\{\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{4}}\\{−\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{2}\:\:\:\:\mathrm{0}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\mathrm{2}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\mathrm{0}\:\:\:\:\mathrm{2}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\begin{pmatrix}{−\mathrm{3}\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{2}}\\{\:\:\:\:\mathrm{0}\:−\mathrm{1}\:\:\:\mathrm{4}\:}\\{−\mathrm{2}\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$${A}\left({A}−\mathrm{2}{I}\right)\:=\:\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{2}}\\{\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{4}}\\{−\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{2}}\\{\:\:\:\mathrm{0}\:\:−\mathrm{1}\:\:\:\:\:\mathrm{4}}\\{−\mathrm{2}\:\:\:\:\mathrm{3}\:\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{10}}\\{−\mathrm{8}\:\:\:\:\mathrm{11}\:\:\:\:\:\mathrm{4}}\\{\:\:\:\mathrm{2}\:\:\:−\mathrm{3}\:\:\:\:\:\:\mathrm{8}}\end{pmatrix} \\ $$$${next}.. \\ $$
