Question Number 114554 by bemath last updated on 19/Sep/20
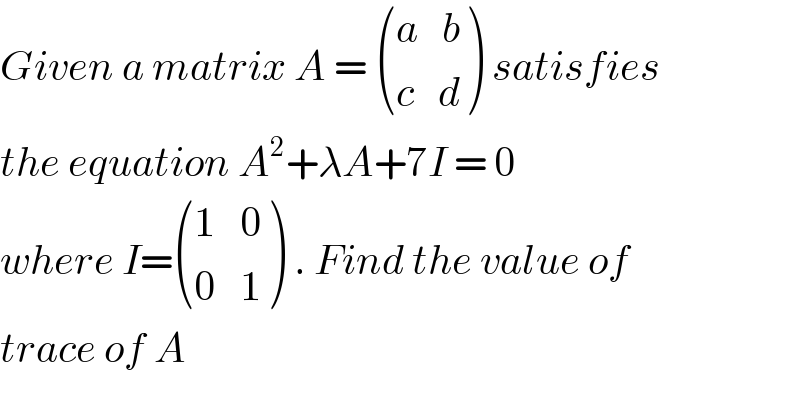
$${Given}\:{a}\:{matrix}\:{A}\:=\:\begin{pmatrix}{{a}\:\:\:{b}}\\{{c}\:\:\:{d}}\end{pmatrix}\:{satisfies} \\ $$$${the}\:{equation}\:{A}^{\mathrm{2}} +\lambda{A}+\mathrm{7}{I}\:=\:\mathrm{0} \\ $$$${where}\:{I}=\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\:.\:{Find}\:{the}\:{value}\:{of}\: \\ $$$${trace}\:{of}\:{A}\: \\ $$
Answered by bobhans last updated on 19/Sep/20
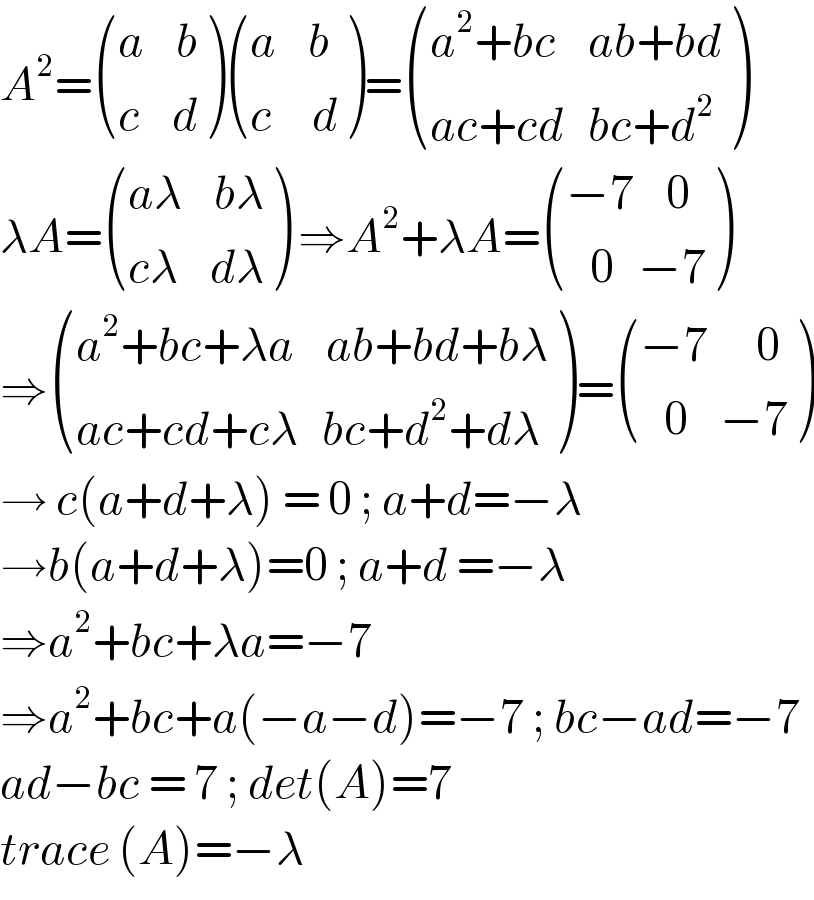
$${A}^{\mathrm{2}} =\begin{pmatrix}{{a}\:\:\:\:{b}}\\{{c}\:\:\:\:{d}}\end{pmatrix}\begin{pmatrix}{{a}\:\:\:\:{b}}\\{{c}\:\:\:\:\:{d}}\end{pmatrix}=\begin{pmatrix}{{a}^{\mathrm{2}} +{bc}\:\:\:\:{ab}+{bd}}\\{{ac}+{cd}\:\:\:{bc}+{d}^{\mathrm{2}} }\end{pmatrix} \\ $$$$\lambda{A}=\begin{pmatrix}{{a}\lambda\:\:\:\:{b}\lambda}\\{{c}\lambda\:\:\:\:{d}\lambda}\end{pmatrix}\:\Rightarrow{A}^{\mathrm{2}} +\lambda{A}=\begin{pmatrix}{−\mathrm{7}\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:−\mathrm{7}}\end{pmatrix} \\ $$$$\Rightarrow\begin{pmatrix}{{a}^{\mathrm{2}} +{bc}+\lambda{a}\:\:\:\:{ab}+{bd}+{b}\lambda}\\{{ac}+{cd}+{c}\lambda\:\:\:{bc}+{d}^{\mathrm{2}} +{d}\lambda}\end{pmatrix}=\begin{pmatrix}{−\mathrm{7}\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:−\mathrm{7}}\end{pmatrix} \\ $$$$\rightarrow\:{c}\left({a}+{d}+\lambda\right)\:=\:\mathrm{0}\:;\:{a}+{d}=−\lambda \\ $$$$\rightarrow{b}\left({a}+{d}+\lambda\right)=\mathrm{0}\:;\:{a}+{d}\:=−\lambda \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{bc}+\lambda{a}=−\mathrm{7} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{bc}+{a}\left(−{a}−{d}\right)=−\mathrm{7}\:;\:{bc}−{ad}=−\mathrm{7} \\ $$$${ad}−{bc}\:=\:\mathrm{7}\:;\:{det}\left({A}\right)=\mathrm{7} \\ $$$${trace}\:\left({A}\right)=−\lambda \\ $$
