Question Number 104544 by john santu last updated on 22/Jul/20
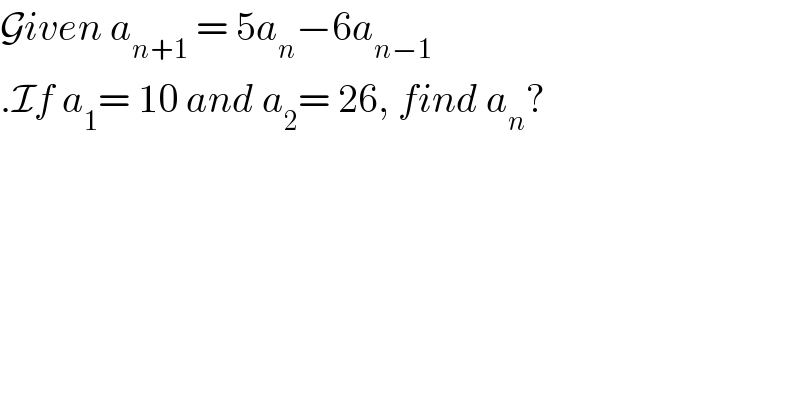
$$\mathcal{G}{iven}\:{a}_{{n}+\mathrm{1}} \:=\:\mathrm{5}{a}_{{n}} −\mathrm{6}{a}_{{n}−\mathrm{1}} \\ $$$$.\mathcal{I}{f}\:{a}_{\mathrm{1}} =\:\mathrm{10}\:{and}\:{a}_{\mathrm{2}} =\:\mathrm{26},\:{find}\:{a}_{{n}} ? \\ $$
Answered by bobhans last updated on 22/Jul/20
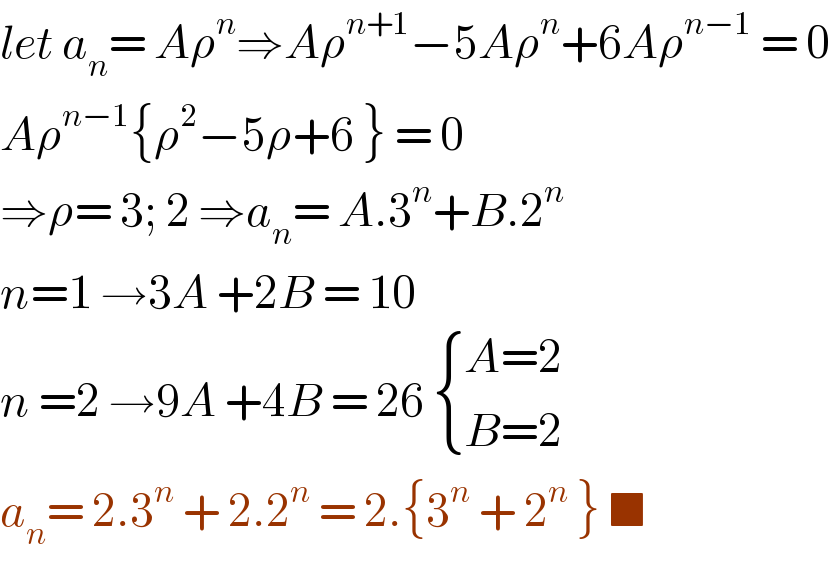
$${let}\:{a}_{{n}} =\:{A}\rho^{{n}} \Rightarrow{A}\rho^{{n}+\mathrm{1}} −\mathrm{5}{A}\rho^{{n}} +\mathrm{6}{A}\rho^{{n}−\mathrm{1}} \:=\:\mathrm{0} \\ $$$${A}\rho^{{n}−\mathrm{1}} \left\{\rho^{\mathrm{2}} −\mathrm{5}\rho+\mathrm{6}\:\right\}\:=\:\mathrm{0} \\ $$$$\Rightarrow\rho=\:\mathrm{3};\:\mathrm{2}\:\Rightarrow{a}_{{n}} =\:{A}.\mathrm{3}^{{n}} +{B}.\mathrm{2}^{{n}} \\ $$$${n}=\mathrm{1}\:\rightarrow\mathrm{3}{A}\:+\mathrm{2}{B}\:=\:\mathrm{10} \\ $$$${n}\:=\mathrm{2}\:\rightarrow\mathrm{9}{A}\:+\mathrm{4}{B}\:=\:\mathrm{26}\:\begin{cases}{{A}=\mathrm{2}}\\{{B}=\mathrm{2}}\end{cases} \\ $$$${a}_{{n}} =\:\mathrm{2}.\mathrm{3}^{{n}} \:+\:\mathrm{2}.\mathrm{2}^{{n}} \:=\:\mathrm{2}.\left\{\mathrm{3}^{{n}} \:+\:\mathrm{2}^{{n}} \:\right\}\:\blacksquare \\ $$
Answered by OlafThorendsen last updated on 22/Jul/20

$${r}^{\mathrm{2}} −\mathrm{5}{r}+\mathrm{6}\:=\:\mathrm{0} \\ $$$$\left({r}−\mathrm{3}\right)\left({r}−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$${r}_{\mathrm{1}} \:=\:\mathrm{2}\:\mathrm{and}\:{r}_{\mathrm{2}} \:=\:\mathrm{3} \\ $$$${a}_{{n}} \:=\:\lambda\mathrm{2}^{{n}} +\mu\mathrm{3}^{{n}} \\ $$$$\mathrm{To}\:\mathrm{find}\:\lambda\:\mathrm{and}\:\mu\: \\ $$$$\mathrm{we}\:\mathrm{use}\:\mathrm{the}\:\mathrm{initial}\:\mathrm{conditions}. \\ $$$${a}_{\mathrm{1}} \:=\:\mathrm{2}\lambda+\mathrm{3}\mu\:=\:\mathrm{10} \\ $$$${a}_{\mathrm{2}} \:=\:\mathrm{4}\lambda+\mathrm{9}\mu\:=\:\mathrm{26} \\ $$$$\Rightarrow\:\lambda\:=\:\mathrm{2}\:\mathrm{and}\:\mu\:=\:\mathrm{2} \\ $$$${a}_{{n}} \:=\:\mathrm{2}.\mathrm{2}^{{n}} +\mathrm{2}.\mathrm{3}^{{n}} \:=\:\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{2}.\mathrm{3}^{{n}} \\ $$
