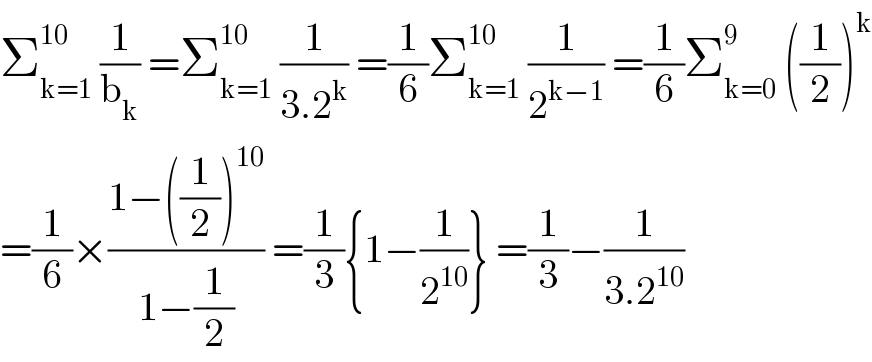Given-b-n-3-2-n-is-a-GP-find-the-value-of-1-b-1-1-b-2-1-b-3-1-b-10-

Question Number 103670 by bobhans last updated on 16/Jul/20

G i v e n b_{n} = 3 . 2^{n} i s a G P . f i n d t h e v a l u e

o f \frac{1}{b_{1}} + \frac{1}{b_{2}} + \frac{1}{b_{3}} + \dots + \frac{1}{b_{10}} ?

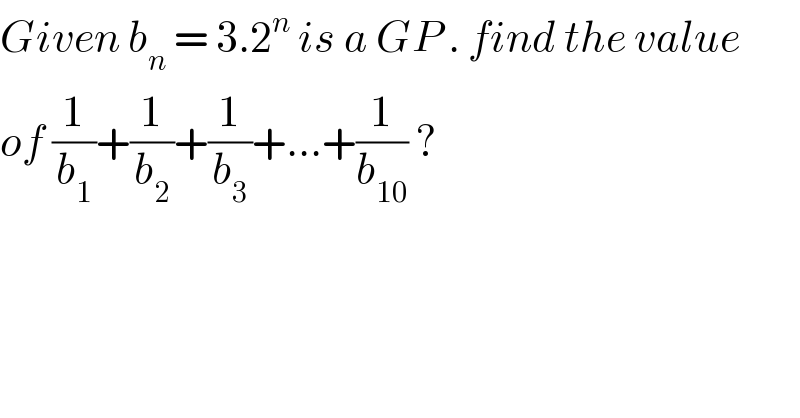
Answered by bramlex last updated on 16/Jul/20

\frac{1}{3.2} + \frac{1}{3.4} + \frac{1}{3.8} + \dots + \frac{1}{3 . 2^{10}} =

\frac{1}{3} {\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots + \frac{1}{2^{10}}} =

\frac{1}{3} {\frac{1}{2} . (\frac{(1 - {(\frac{1}{2})}^{10}}{\frac{1}{2}})} =

\frac{1}{3} . {\frac{2^{10} - 1}{2^{10}}} = \frac{1023}{3 \times 1024} = \frac{341}{1024} ⊛

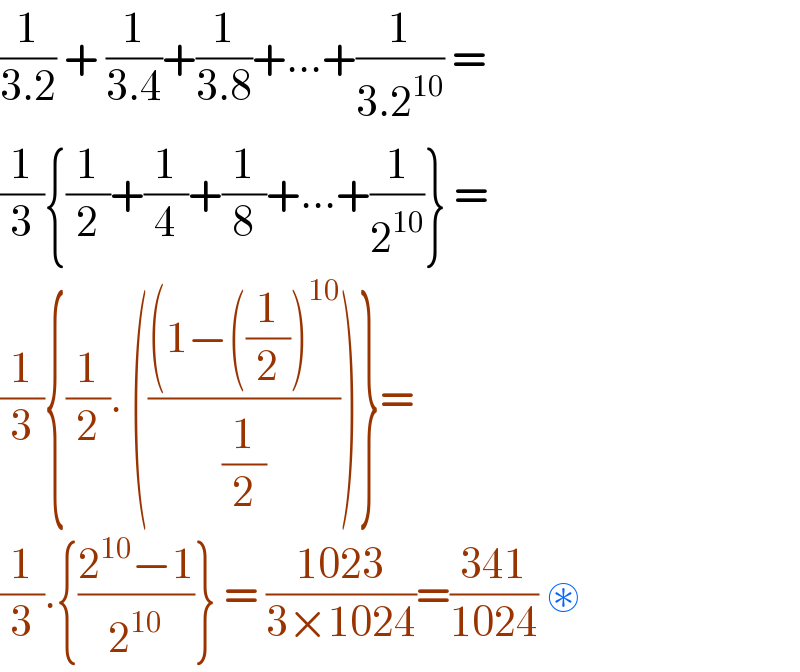
Answered by Worm_Tail last updated on 16/Jul/20

b_{n} = 3 . 2^{n} \Rightarrow \frac{1}{b_{n}} = \frac{1}{3 {(2)}^{n}}

Σ \frac{1}{b_{n}} = Σ \frac{1}{3 {(2)}^{n}} = \frac{1}{3} Σ {(\frac{1}{2})}^{n}

Σ \frac{1}{b_{n}} = \frac{1}{3} Σ {(\frac{1}{2})}^{n} = \frac{1}{6} (\frac{1 - 2^{- n}}{0.5})

Σ \frac{1}{b_{n}} = \frac{1}{3} (1 - 2^{- n}) n = 10

Σ \frac{1}{b_{n}} = \frac{1}{3} (1 - 2^{- 10}) = \frac{341}{1024}

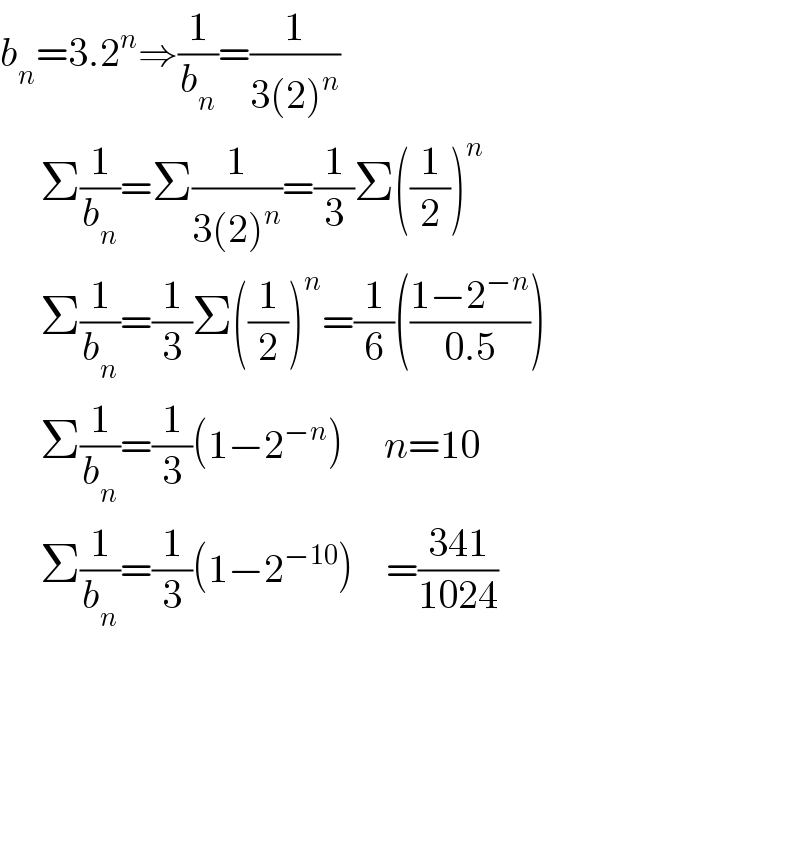
Answered by Dwaipayan Shikari last updated on 16/Jul/20

\frac{1}{3.2} + \frac{1}{3 . 2^{2}} + \frac{1}{3 . 2^{3}} + \dots + n = \frac{1}{3} . \frac{1}{2} (\frac{{(\frac{1}{2})}^{n} - 1}{\frac{1}{2} - 1}) = \frac{1}{3} (1 - 2^{- n}) = \frac{1}{3} . \frac{1023}{1024} = \frac{341}{1024}

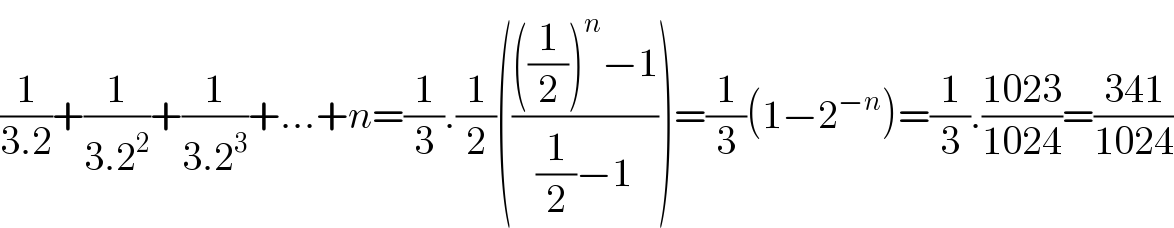
Answered by mathmax by abdo last updated on 16/Jul/20

\sum_{k = 1}^{10} \frac{1}{b_{k}} = \sum_{k = 1}^{10} \frac{1}{3 . 2^{k}} = \frac{1}{6} \sum_{k = 1}^{10} \frac{1}{2^{k - 1}} = \frac{1}{6} \sum_{k = 0}^{9} {(\frac{1}{2})}^{k}

= \frac{1}{6} \times \frac{1 - {(\frac{1}{2})}^{10}}{1 - \frac{1}{2}} = \frac{1}{3} {1 - \frac{1}{2^{10}}} = \frac{1}{3} - \frac{1}{3 . 2^{10}}