Question Number 82521 by jagoll last updated on 22/Feb/20

$${given}\:\frac{{dy}}{{dx}}\:=\:{xy}^{\mathrm{3}} \\ $$$${Determine}\:{the}\:{concavity}\:{of}\:{all} \\ $$$${solution}\:{curves}\:{for}\:{the}\:{given}\: \\ $$$${differential}\:{equation}\:{in}\: \\ $$$${quadrant}\:{iv}.\: \\ $$
Commented by jagoll last updated on 22/Feb/20

$${someone}\:{maybe}\:{help}\:{me} \\ $$
Commented by mr W last updated on 22/Feb/20

$$\frac{{dy}}{{dx}}={xy}^{\mathrm{3}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={y}^{\mathrm{3}} +\mathrm{3}{xy}^{\mathrm{2}} \frac{{dy}}{{dx}}={y}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right) \\ $$$${in}\:{quadrant}\:{iii}\:{and}\:{iv}:\:\:{y}<\mathrm{0} \\ $$$$\Rightarrow\:{y}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)<\mathrm{0} \\ $$$$\Rightarrow\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }<\mathrm{0} \\ $$$$\Rightarrow{all}\:{solution}\:{curves}\:{are}\:{concave}\:{here}! \\ $$$$ \\ $$$${we}\:{even}\:{don}'{t}\:{need}\:{to}\:{solve}\:{the}\:{d}.\:{eqn}. \\ $$
Commented by mr W last updated on 22/Feb/20
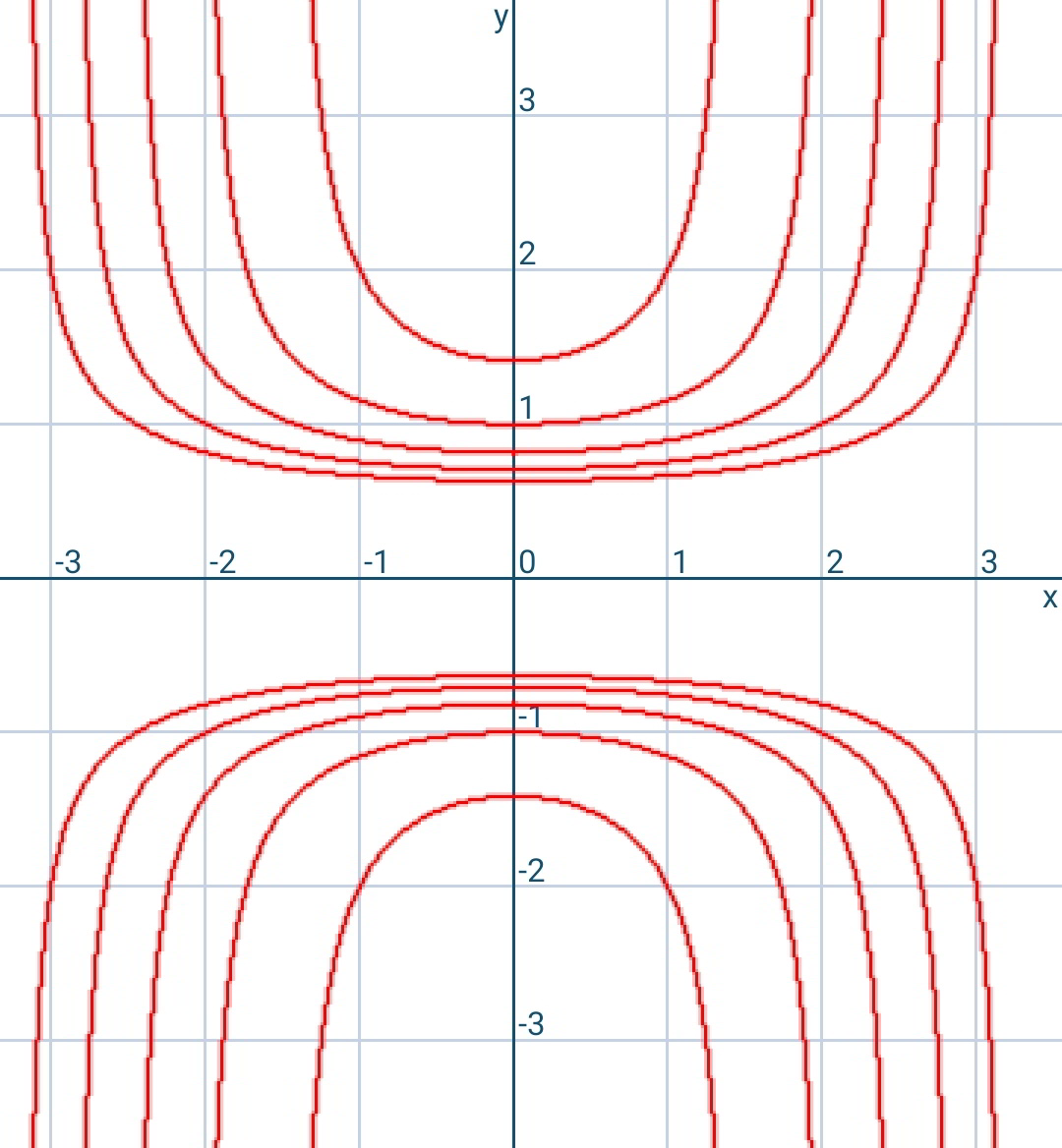
Commented by mr W last updated on 22/Feb/20

$${these}\:{are}\:{some}\:{examples}\:{from}\:{the} \\ $$$${solution}\:{curves}. \\ $$
Commented by jagoll last updated on 22/Feb/20

$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:{y}^{\mathrm{3}} \:+\:\mathrm{3}{xy}^{\mathrm{2}} \:\frac{{dy}}{{dx}\:} \\ $$$${sir}? \\ $$
Commented by mr W last updated on 22/Feb/20

$${yes}\:{sir}!\:{now}\:{it}'{s}\:{fixed}.\:{thanks}\:{alot}! \\ $$
Commented by john santu last updated on 22/Feb/20
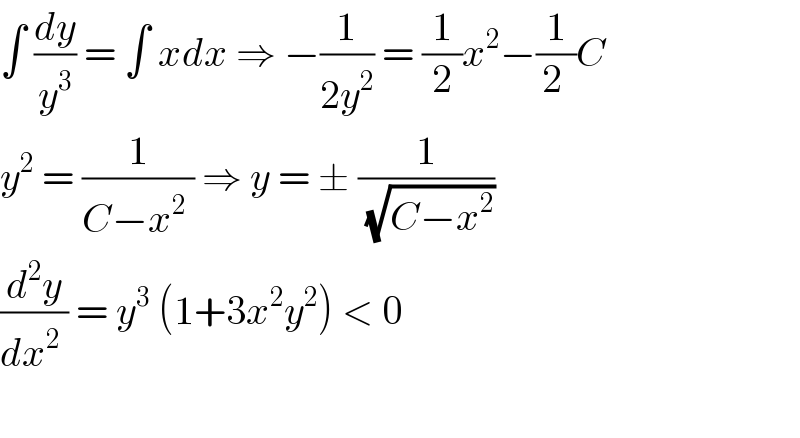
$$\int\:\frac{{dy}}{{y}^{\mathrm{3}} }\:=\:\int\:{xdx}\:\Rightarrow\:−\frac{\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}\:}{C} \\ $$$${y}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{{C}−{x}^{\mathrm{2}} \:}\:\Rightarrow\:{y}\:=\:\pm\:\frac{\mathrm{1}}{\:\sqrt{{C}−{x}^{\mathrm{2}} }}\: \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} \:}\:=\:{y}^{\mathrm{3}} \:\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)\:<\:\mathrm{0}\: \\ $$$$ \\ $$
