Menu Close

Given-f-2x-3-2x-1-f-2x-3-1-2x-4x-f-x-

Tinku Tara 0 Comments
Pin




Question Number 150044 by bramlexs22 last updated on 09/Aug/21
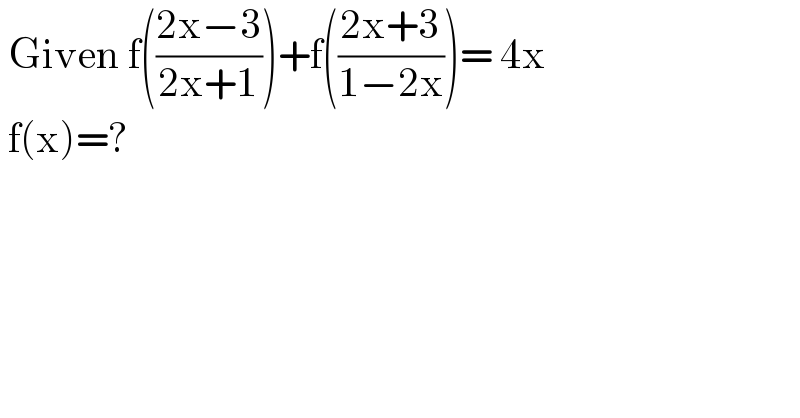
Given f(((2x−3)/(2x+1)))+f(((2x+3)/(1−2x)))= 4x f(x)=?
$$\:\mathrm{Given}\:\mathrm{f}\left(\frac{\mathrm{2x}−\mathrm{3}}{\mathrm{2x}+\mathrm{1}}\right)+\mathrm{f}\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{1}−\mathrm{2x}}\right)=\:\mathrm{4x} \\ $$$$\:\mathrm{f}\left(\mathrm{x}\right)=? \\ $$
Answered by liberty last updated on 09/Aug/21
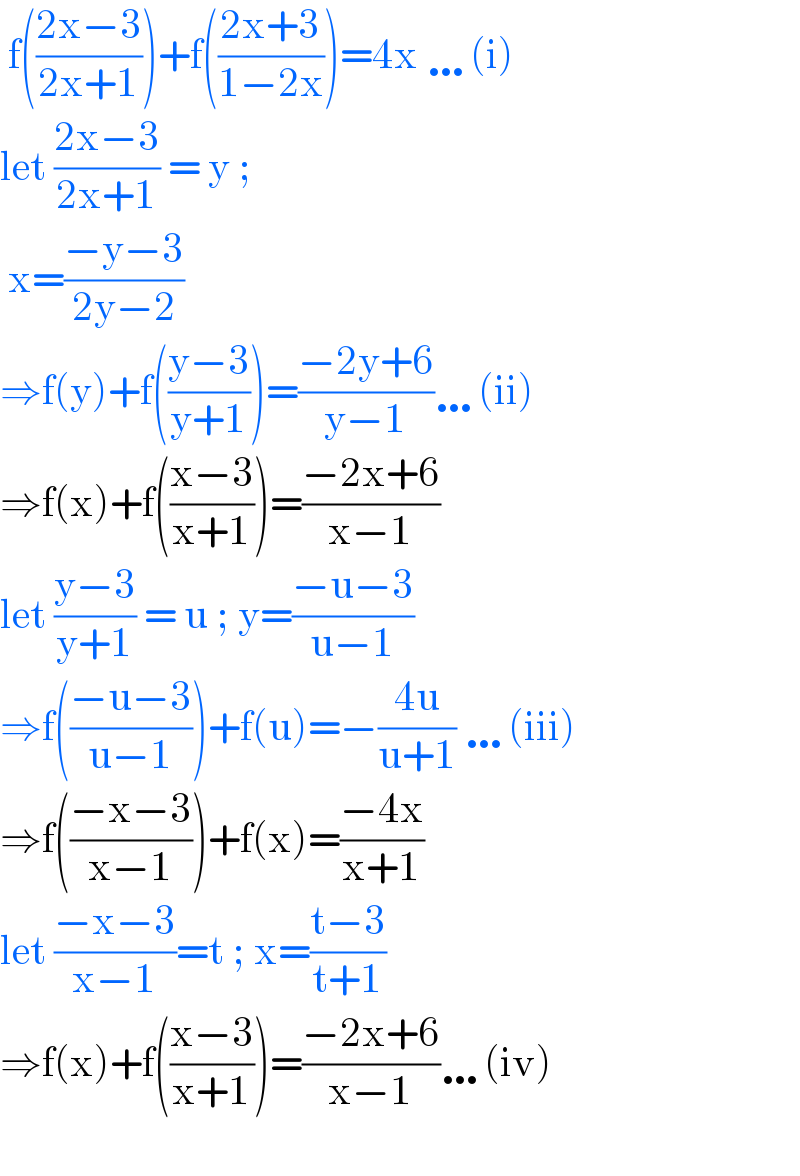
f(((2x−3)/(2x+1)))+f(((2x+3)/(1−2x)))=4x …(i) let ((2x−3)/(2x+1)) = y ; x=((−y−3)/(2y−2)) ⇒f(y)+f(((y−3)/(y+1)))=((−2y+6)/(y−1))…(ii) ⇒f(x)+f(((x−3)/(x+1)))=((−2x+6)/(x−1)) let ((y−3)/(y+1)) = u ; y=((−u−3)/(u−1)) ⇒f(((−u−3)/(u−1)))+f(u)=−((4u)/(u+1)) …(iii) ⇒f(((−x−3)/(x−1)))+f(x)=((−4x)/(x+1)) let ((−x−3)/(x−1))=t ; x=((t−3)/(t+1)) ⇒f(x)+f(((x−3)/(x+1)))=((−2x+6)/(x−1))…(iv)
$$\:\mathrm{f}\left(\frac{\mathrm{2x}−\mathrm{3}}{\mathrm{2x}+\mathrm{1}}\right)+\mathrm{f}\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{1}−\mathrm{2x}}\right)=\mathrm{4x}\:\ldots\left(\mathrm{i}\right) \\ $$$$\mathrm{let}\:\frac{\mathrm{2x}−\mathrm{3}}{\mathrm{2x}+\mathrm{1}}\:=\:\mathrm{y}\:; \\ $$$$\:\mathrm{x}=\frac{−\mathrm{y}−\mathrm{3}}{\mathrm{2y}−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{y}\right)+\mathrm{f}\left(\frac{\mathrm{y}−\mathrm{3}}{\mathrm{y}+\mathrm{1}}\right)=\frac{−\mathrm{2y}+\mathrm{6}}{\mathrm{y}−\mathrm{1}}\ldots\left(\mathrm{ii}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{1}}\right)=\frac{−\mathrm{2x}+\mathrm{6}}{\mathrm{x}−\mathrm{1}} \\ $$$$\mathrm{let}\:\frac{\mathrm{y}−\mathrm{3}}{\mathrm{y}+\mathrm{1}}\:=\:\mathrm{u}\:;\:\mathrm{y}=\frac{−\mathrm{u}−\mathrm{3}}{\mathrm{u}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}\left(\frac{−\mathrm{u}−\mathrm{3}}{\mathrm{u}−\mathrm{1}}\right)+\mathrm{f}\left(\mathrm{u}\right)=−\frac{\mathrm{4u}}{\mathrm{u}+\mathrm{1}}\:\ldots\left(\mathrm{iii}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\frac{−\mathrm{x}−\mathrm{3}}{\mathrm{x}−\mathrm{1}}\right)+\mathrm{f}\left(\mathrm{x}\right)=\frac{−\mathrm{4x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{let}\:\frac{−\mathrm{x}−\mathrm{3}}{\mathrm{x}−\mathrm{1}}=\mathrm{t}\:;\:\mathrm{x}=\frac{\mathrm{t}−\mathrm{3}}{\mathrm{t}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{1}}\right)=\frac{−\mathrm{2x}+\mathrm{6}}{\mathrm{x}−\mathrm{1}}\ldots\left(\mathrm{iv}\right) \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 09/Aug/21
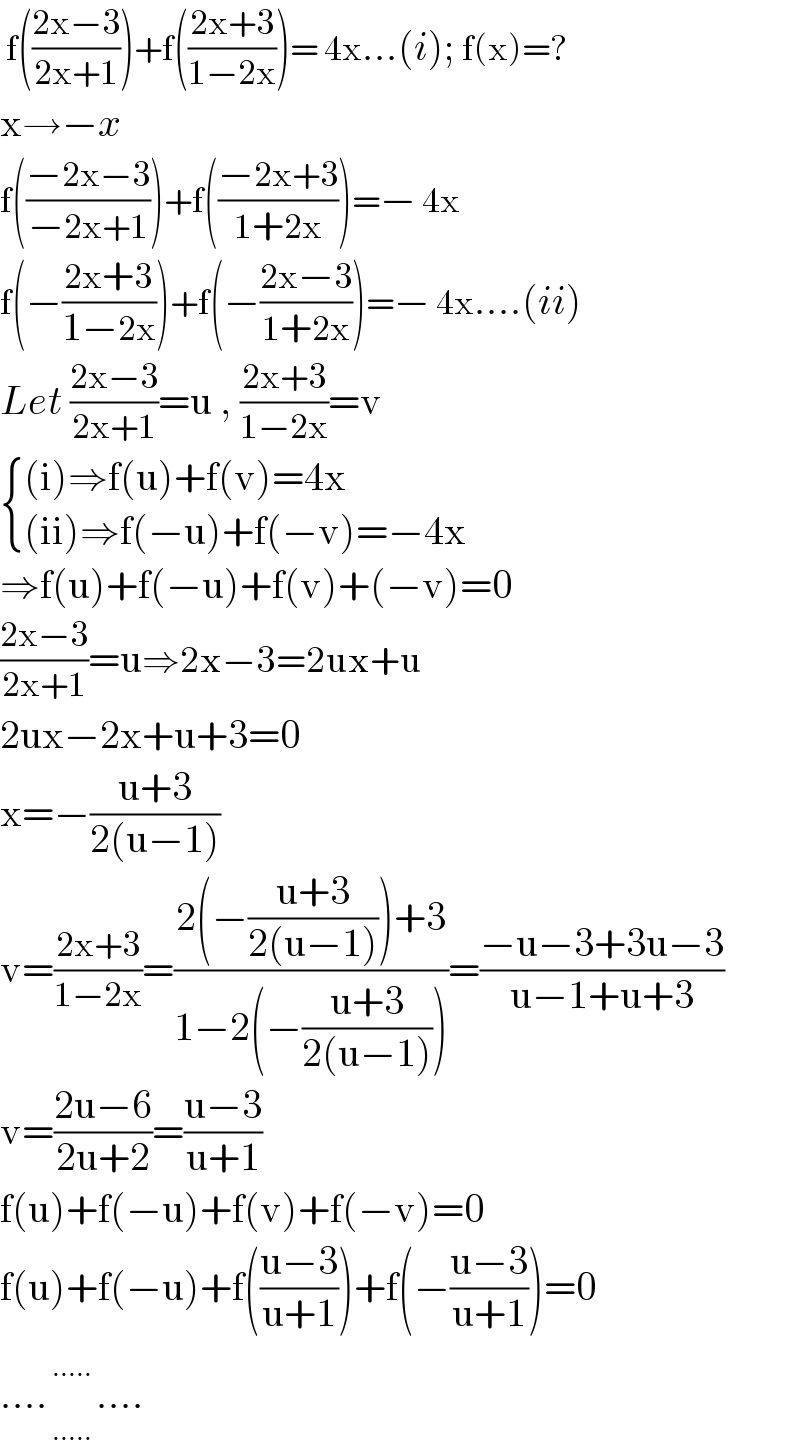
f(((2x−3)/(2x+1)))+f(((2x+3)/(1−2x)))= 4x...(i); f(x)=? x→−x f(((−2x−3)/(−2x+1)))+f(((−2x+3)/(1+2x)))=− 4x f(−((2x+3)/(1−2x)))+f(−((2x−3)/(1+2x)))=− 4x....(ii) Let ((2x−3)/(2x+1))=u , ((2x+3)/(1−2x))=v { (((i)⇒f(u)+f(v)=4x)),(((ii)⇒f(−u)+f(−v)=−4x)) :} ⇒f(u)+f(−u)+f(v)+(−v)=0 ((2x−3)/(2x+1))=u⇒2x−3=2ux+u 2ux−2x+u+3=0 x=−((u+3)/(2(u−1))) v=((2x+3)/(1−2x))=((2(−((u+3)/(2(u−1))))+3)/(1−2(−((u+3)/(2(u−1))))))=((−u−3+3u−3)/(u−1+u+3)) v=((2u−6)/(2u+2))=((u−3)/(u+1)) f(u)+f(−u)+f(v)+f(−v)=0 f(u)+f(−u)+f(((u−3)/(u+1)))+f(−((u−3)/(u+1)))=0 .... _(.....) ^(.....) ....
$$\:\mathrm{f}\left(\frac{\mathrm{2x}−\mathrm{3}}{\mathrm{2x}+\mathrm{1}}\right)+\mathrm{f}\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{1}−\mathrm{2x}}\right)=\:\mathrm{4x}…\left({i}\right);\:\mathrm{f}\left(\mathrm{x}\right)=? \\ $$$$\mathrm{x}\rightarrow−{x} \\ $$$$\mathrm{f}\left(\frac{−\mathrm{2x}−\mathrm{3}}{−\mathrm{2x}+\mathrm{1}}\right)+\mathrm{f}\left(\frac{−\mathrm{2x}+\mathrm{3}}{\mathrm{1}+\mathrm{2x}}\right)=−\:\mathrm{4x} \\ $$$$\mathrm{f}\left(−\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{1}−\mathrm{2x}}\right)+\mathrm{f}\left(−\frac{\mathrm{2x}−\mathrm{3}}{\mathrm{1}+\mathrm{2x}}\right)=−\:\mathrm{4x}….\left({ii}\right) \\ $$$${Let}\:\frac{\mathrm{2x}−\mathrm{3}}{\mathrm{2x}+\mathrm{1}}=\mathrm{u}\:,\:\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{1}−\mathrm{2x}}=\mathrm{v} \\ $$$$\begin{cases}{\left(\mathrm{i}\right)\Rightarrow\mathrm{f}\left(\mathrm{u}\right)+\mathrm{f}\left(\mathrm{v}\right)=\mathrm{4x}}\\{\left(\mathrm{ii}\right)\Rightarrow\mathrm{f}\left(−\mathrm{u}\right)+\mathrm{f}\left(−\mathrm{v}\right)=−\mathrm{4x}}\end{cases} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{u}\right)+\mathrm{f}\left(−\mathrm{u}\right)+\mathrm{f}\left(\mathrm{v}\right)+\left(−\mathrm{v}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{2x}−\mathrm{3}}{\mathrm{2x}+\mathrm{1}}=\mathrm{u}\Rightarrow\mathrm{2x}−\mathrm{3}=\mathrm{2ux}+\mathrm{u} \\ $$$$\mathrm{2ux}−\mathrm{2x}+\mathrm{u}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{x}=−\frac{\mathrm{u}+\mathrm{3}}{\mathrm{2}\left(\mathrm{u}−\mathrm{1}\right)} \\ $$$$\mathrm{v}=\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{1}−\mathrm{2x}}=\frac{\mathrm{2}\left(−\frac{\mathrm{u}+\mathrm{3}}{\mathrm{2}\left(\mathrm{u}−\mathrm{1}\right)}\right)+\mathrm{3}}{\mathrm{1}−\mathrm{2}\left(−\frac{\mathrm{u}+\mathrm{3}}{\mathrm{2}\left(\mathrm{u}−\mathrm{1}\right)}\right)}=\frac{−\mathrm{u}−\mathrm{3}+\mathrm{3u}−\mathrm{3}}{\mathrm{u}−\mathrm{1}+\mathrm{u}+\mathrm{3}} \\ $$$$\mathrm{v}=\frac{\mathrm{2u}−\mathrm{6}}{\mathrm{2u}+\mathrm{2}}=\frac{\mathrm{u}−\mathrm{3}}{\mathrm{u}+\mathrm{1}} \\ $$$$\mathrm{f}\left(\mathrm{u}\right)+\mathrm{f}\left(−\mathrm{u}\right)+\mathrm{f}\left(\mathrm{v}\right)+\mathrm{f}\left(−\mathrm{v}\right)=\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{u}\right)+\mathrm{f}\left(−\mathrm{u}\right)+\mathrm{f}\left(\frac{\mathrm{u}−\mathrm{3}}{\mathrm{u}+\mathrm{1}}\right)+\mathrm{f}\left(−\frac{\mathrm{u}−\mathrm{3}}{\mathrm{u}+\mathrm{1}}\right)=\mathrm{0} \\ $$$$….\underset{…..} {\overset{…..} {\:\:\:\:\:\:}}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *