Question Number 123386 by bemath last updated on 25/Nov/20
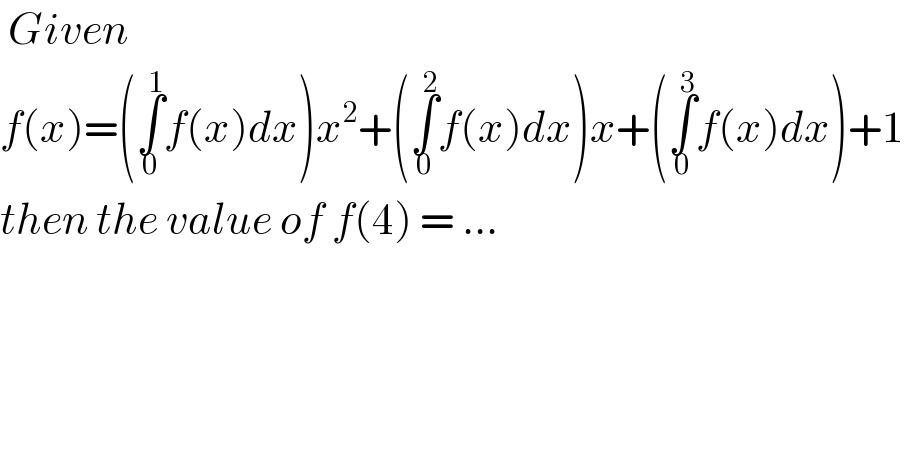
$$\:{Given}\: \\ $$$${f}\left({x}\right)=\left(\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}\right){x}^{\mathrm{2}} +\left(\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{f}\left({x}\right){dx}\right){x}+\left(\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}{f}\left({x}\right){dx}\right)+\mathrm{1} \\ $$$${then}\:{the}\:{value}\:{of}\:{f}\left(\mathrm{4}\right)\:=\:… \\ $$
Answered by TANMAY PANACEA last updated on 25/Nov/20

$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}+\mathrm{1} \\ $$$${a}=\int_{\mathrm{0}} ^{\mathrm{1}} \left({ax}^{\mathrm{2}} +{bx}+{c}+\mathrm{1}\right)\:\:{dx} \\ $$$${a}=\mid\frac{{ax}^{\mathrm{3}} }{\mathrm{3}}+\frac{{bx}^{\mathrm{2}} }{\mathrm{2}}+{cx}+{x}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${a}=\frac{{a}}{\mathrm{3}}+\frac{{b}}{\mathrm{2}}+{c}+\mathrm{1}…..\left(\mathrm{1}{st}\:{eqn}\right) \\ $$$${b}=\mid\frac{{ax}^{\mathrm{3}} }{\mathrm{3}}+\frac{{bx}^{\mathrm{2}} }{\mathrm{2}}+{cx}+{x}\mid_{\mathrm{0}} ^{\mathrm{2}} \\ $$$${b}=\frac{\mathrm{8}{a}}{\mathrm{3}}+\frac{\mathrm{4}{b}}{\mathrm{2}}+\mathrm{2}{c}+\mathrm{2}….+\left(\mathrm{2}{nd}\:{eqn}\right) \\ $$$${c}=\mid\frac{{ax}^{\mathrm{3}} }{\mathrm{3}}+\frac{{bx}^{\mathrm{2}} }{\mathrm{2}}+{cx}+{x}\mid_{\mathrm{0}} ^{\mathrm{3}} \\ $$$${c}=\frac{\mathrm{27}{a}}{\mathrm{3}}+\frac{\mathrm{9}{b}}{\mathrm{4}}+\mathrm{3}{c}+\mathrm{3}….\left(\mathrm{3}{rd}\:{eqn}\right) \\ $$$${we}\:{have}\:{to}\:{solve}\:\:{to}\:{find}\:\left({a},{b}\:{and}\:{c}\right) \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}+\mathrm{1} \\ $$$${nxt}\:{to}\:{put}\:{x}=\mathrm{4} \\ $$$$ \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{try}}\:\boldsymbol{{from}}\:\boldsymbol{{here}}.. \\ $$
