Question Number 101008 by Rio Michael last updated on 29/Jun/20
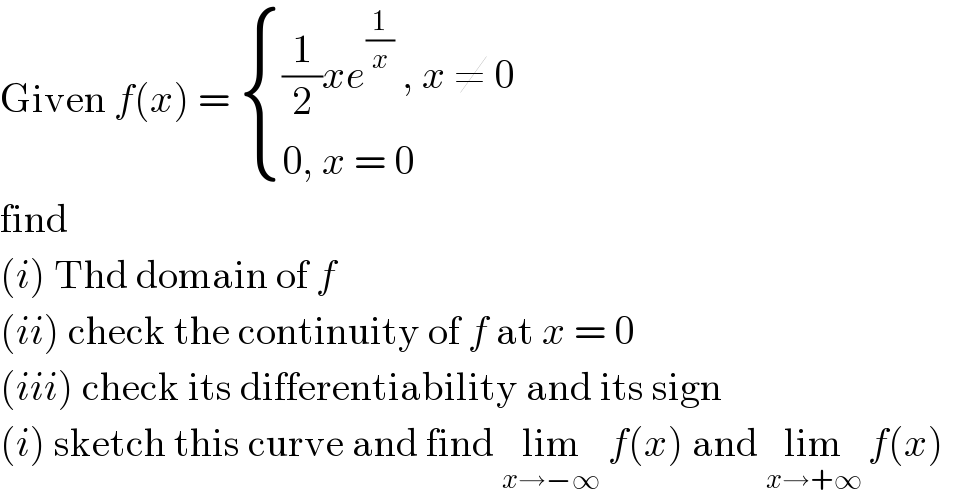
$$\mathrm{Given}\:{f}\left({x}\right)\:=\:\begin{cases}{\frac{\mathrm{1}}{\mathrm{2}}{xe}^{\frac{\mathrm{1}}{{x}}} \:,\:{x}\:\neq\:\mathrm{0}}\\{\mathrm{0},\:{x}\:=\:\mathrm{0}\:}\end{cases} \\ $$$$\mathrm{find} \\ $$$$\left({i}\right)\:\mathrm{Thd}\:\mathrm{domain}\:\mathrm{of}\:{f} \\ $$$$\left({ii}\right)\:\mathrm{check}\:\mathrm{the}\:\mathrm{continuity}\:\mathrm{of}\:{f}\:\mathrm{at}\:{x}\:=\:\mathrm{0} \\ $$$$\left({iii}\right)\:\mathrm{check}\:\mathrm{its}\:\mathrm{differentiability}\:\mathrm{and}\:\mathrm{its}\:\mathrm{sign} \\ $$$$\left({i}\right)\:\mathrm{sketch}\:\mathrm{this}\:\mathrm{curve}\:\mathrm{and}\:\mathrm{find}\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{f}\left({x}\right)\:\mathrm{and}\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:{f}\left({x}\right) \\ $$
Answered by maths mind last updated on 29/Jun/20
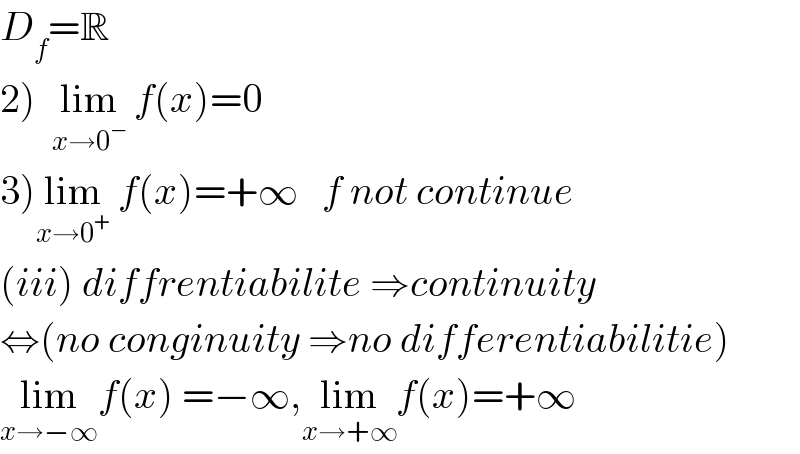
$${D}_{{f}} =\mathbb{R} \\ $$$$\left.\mathrm{2}\right)\:\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{f}\left({x}\right)=+\infty\:\:\:{f}\:{not}\:{continue} \\ $$$$\left({iii}\right)\:{diffrentiabilite}\:\Rightarrow{continuity} \\ $$$$\Leftrightarrow\left({no}\:{conginuity}\:\Rightarrow{no}\:{differentiabilitie}\right) \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}{f}\left({x}\right)\:=−\infty,\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)=+\infty \\ $$
