Menu Close

Given-f-x-1-x-x-2-x-3-x-2015-x-2016-2-Find-the-sum-of-all-odd-coeffisiens-Ex-f-x-x-2-x-1-2-1x-4-2x-3-3x-2-2x-1-The-sum-of-odd-coeffisien-is-1-

Tinku Tara 0 Comments
Pin




Question Number 26087 by Joel578 last updated on 19/Dec/17
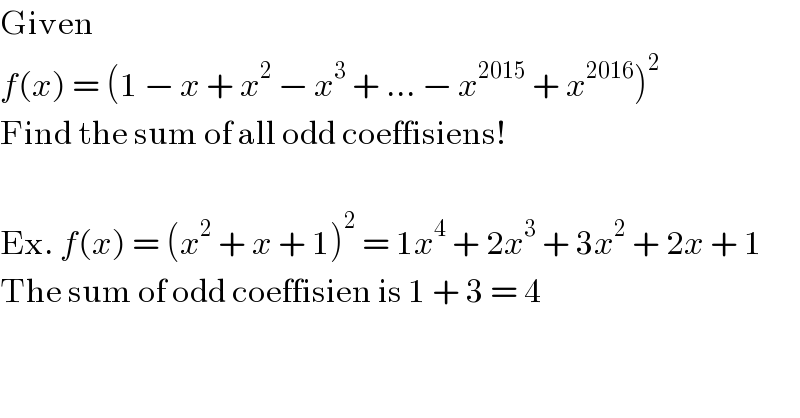
Given f(x) = (1 − x + x^2 − x^3 + ... − x^(2015) + x^(2016) )^2 Find the sum of all odd coeffisiens! Ex. f(x) = (x^2 + x + 1)^2 = 1x^4 + 2x^3 + 3x^2 + 2x + 1 The sum of odd coeffisien is 1 + 3 = 4
$$\mathrm{Given} \\ $$$${f}\left({x}\right)\:=\:\left(\mathrm{1}\:−\:{x}\:+\:{x}^{\mathrm{2}} \:−\:{x}^{\mathrm{3}} \:+\:…\:−\:{x}^{\mathrm{2015}} \:+\:{x}^{\mathrm{2016}} \right)^{\mathrm{2}} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{odd}\:\mathrm{coeffisiens}! \\ $$$$ \\ $$$$\mathrm{Ex}.\:{f}\left({x}\right)\:=\:\left({x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{1}{x}^{\mathrm{4}} \:+\:\mathrm{2}{x}^{\mathrm{3}} \:+\:\mathrm{3}{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:+\:\mathrm{1} \\ $$$$\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{coeffisien}\:\mathrm{is}\:\mathrm{1}\:+\:\mathrm{3}\:=\:\mathrm{4} \\ $$
Commented by moxhix last updated on 19/Dec/17
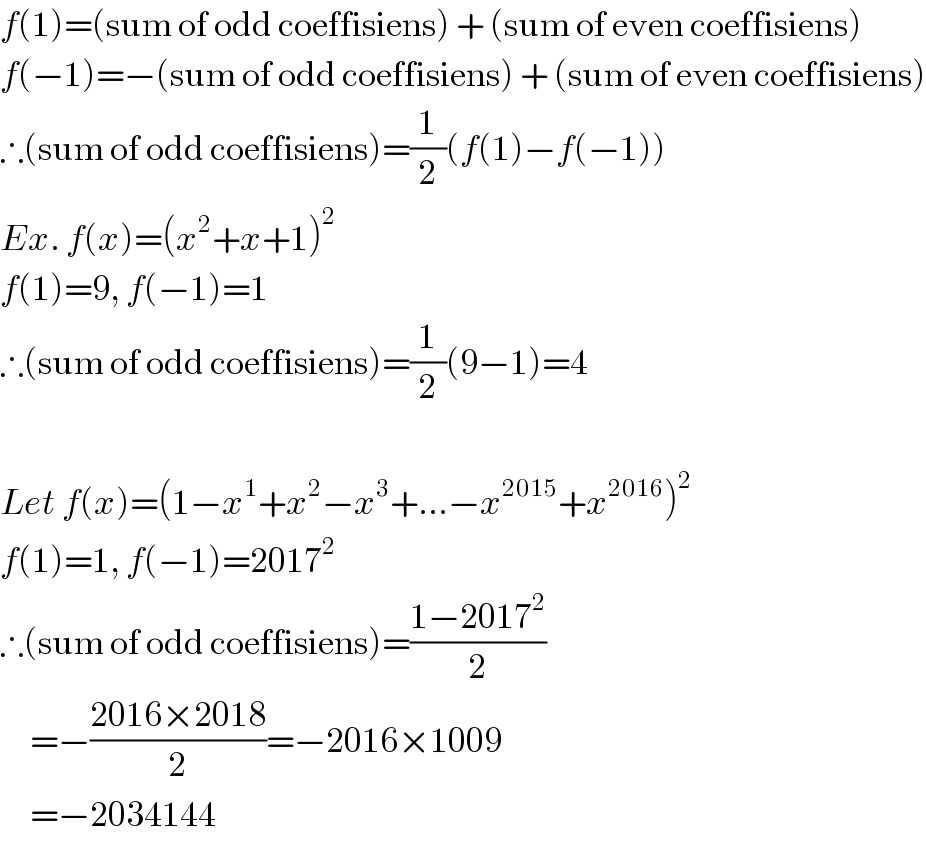
f(1)=(sum of odd coeffisiens) + (sum of even coeffisiens) f(−1)=−(sum of odd coeffisiens) + (sum of even coeffisiens) ∴(sum of odd coeffisiens)=(1/2)(f(1)−f(−1)) Ex. f(x)=(x^2 +x+1)^2 f(1)=9, f(−1)=1 ∴(sum of odd coeffisiens)=(1/2)(9−1)=4 Let f(x)=(1−x^1 +x^2 −x^3 +...−x^(2015) +x^(2016) )^2 f(1)=1, f(−1)=2017^2 ∴(sum of odd coeffisiens)=((1−2017^2 )/2) =−((2016×2018)/2)=−2016×1009 =−2034144
$${f}\left(\mathrm{1}\right)=\left(\mathrm{sum}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{coeffisiens}\right)\:+\:\left(\mathrm{sum}\:\mathrm{of}\:\mathrm{even}\:\mathrm{coeffisiens}\right) \\ $$$${f}\left(−\mathrm{1}\right)=−\left(\mathrm{sum}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{coeffisiens}\right)\:+\:\left(\mathrm{sum}\:\mathrm{of}\:\mathrm{even}\:\mathrm{coeffisiens}\right) \\ $$$$\therefore\left(\mathrm{sum}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{coeffisiens}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({f}\left(\mathrm{1}\right)−{f}\left(−\mathrm{1}\right)\right) \\ $$$${Ex}.\:{f}\left({x}\right)=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{9},\:{f}\left(−\mathrm{1}\right)=\mathrm{1} \\ $$$$\therefore\left(\mathrm{sum}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{coeffisiens}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{9}−\mathrm{1}\right)=\mathrm{4} \\ $$$$ \\ $$$${Let}\:{f}\left({x}\right)=\left(\mathrm{1}−{x}^{\mathrm{1}} +{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +…−{x}^{\mathrm{2015}} +{x}^{\mathrm{2016}} \right)^{\mathrm{2}} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1},\:{f}\left(−\mathrm{1}\right)=\mathrm{2017}^{\mathrm{2}} \\ $$$$\therefore\left(\mathrm{sum}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{coeffisiens}\right)=\frac{\mathrm{1}−\mathrm{2017}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{2016}×\mathrm{2018}}{\mathrm{2}}=−\mathrm{2016}×\mathrm{1009} \\ $$$$\:\:\:\:\:=−\mathrm{2034144} \\ $$
Commented by moxhix last updated on 19/Dec/17
I′m sorry, I misundertood....
$$\mathrm{I}'\mathrm{m}\:\mathrm{sorry},\:\mathrm{I}\:\mathrm{misundertood}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *