Question Number 128221 by john_santu last updated on 05/Jan/21
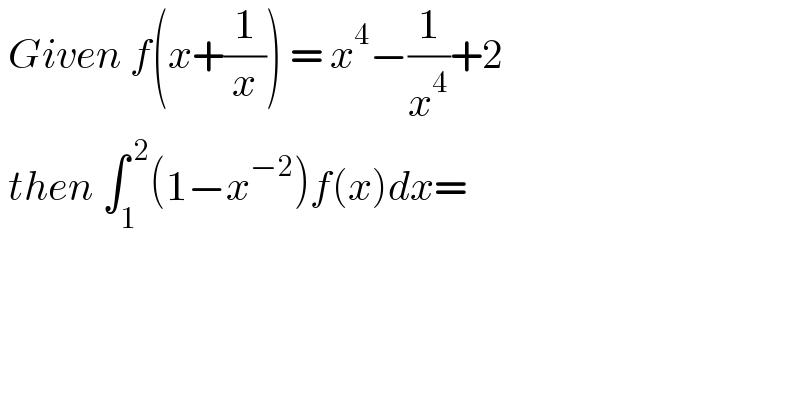
$$\:{Given}\:{f}\left({x}+\frac{\mathrm{1}}{{x}}\right)\:=\:{x}^{\mathrm{4}} −\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\mathrm{2} \\ $$$$\:{then}\:\int_{\mathrm{1}} ^{\:\mathrm{2}} \left(\mathrm{1}−{x}^{−\mathrm{2}} \right){f}\left({x}\right){dx}= \\ $$
Answered by liberty last updated on 05/Jan/21
)(x−(1/x))+2 (•) x−(1/x) = (√((x−(1/x))^2 )) = (√((x+(1/x))^2 −4)) then f(x+(1/x))=[(x+(1/x))^2 −2 ](x+(1/x))(√((x+(1/x))^2 −4)) +2 or f(x) = (x^2 −2)x(√(x^2 −4)) +2 then ∫_1 ^( 2) (((x^2 −1)/x^2 ))[ x(x^2 −2)(√(x^2 −4)) +2 ] dx= ∫_1 ^( 2) (((x^2 −1)(x^2 −2)(√(x^2 −4)))/x) dx−∫_1 ^( 2) ((2(x^2 −1))/x^2 ) dx I_1 = ∫_1 ^( 2) (((x^4 −3x^2 +2)(√(x^2 −4)))/x) dx I_2 = ∫_1 ^( 2) 2(1−x^(−2) ) dx](https://www.tinkutara.com/question/Q128223.png)
$${x}^{\mathrm{4}} −\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:+\mathrm{2}\:=\:\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\mathrm{2} \\ $$$$\:=\:\left[\:\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}\:\right]\left({x}+\frac{\mathrm{1}}{{x}}\right)\left({x}−\frac{\mathrm{1}}{{x}}\right)+\mathrm{2} \\ $$$$\:\left(\bullet\right)\:{x}−\frac{\mathrm{1}}{{x}}\:=\:\sqrt{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }\:=\:\sqrt{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{4}} \\ $$$${then}\:{f}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\left[\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}\:\right]\left({x}+\frac{\mathrm{1}}{{x}}\right)\sqrt{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{4}}\:+\mathrm{2} \\ $$$${or}\:{f}\left({x}\right)\:=\:\left({x}^{\mathrm{2}} −\mathrm{2}\right){x}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\:+\mathrm{2}\: \\ $$$${then}\:\int_{\mathrm{1}} ^{\:\mathrm{2}} \:\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left[\:{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\:+\mathrm{2}\:\right]\:{dx}= \\ $$$$\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}}{{x}}\:{dx}−\int_{\mathrm{1}} ^{\:\mathrm{2}} \:\frac{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}^{\mathrm{2}} }\:{dx} \\ $$$${I}_{\mathrm{1}} =\:\int_{\mathrm{1}} ^{\:\mathrm{2}} \:\frac{\left({x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}}{{x}}\:{dx} \\ $$$$\:{I}_{\mathrm{2}} \:=\:\int_{\mathrm{1}} ^{\:\mathrm{2}} \:\mathrm{2}\left(\mathrm{1}−{x}^{−\mathrm{2}} \right)\:{dx}\: \\ $$
