Question Number 167925 by naka3546 last updated on 29/Mar/22
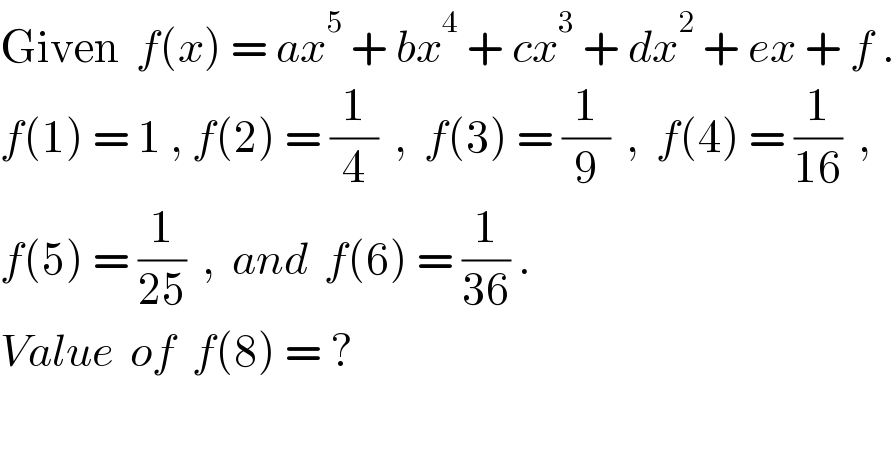
$$\mathrm{Given}\:\:{f}\left({x}\right)\:=\:{ax}^{\mathrm{5}} \:+\:{bx}^{\mathrm{4}} \:+\:{cx}^{\mathrm{3}} \:+\:{dx}^{\mathrm{2}} \:+\:{ex}\:+\:{f}\:. \\ $$$${f}\left(\mathrm{1}\right)\:=\:\mathrm{1}\:,\:{f}\left(\mathrm{2}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\:,\:\:{f}\left(\mathrm{3}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\:,\:\:{f}\left(\mathrm{4}\right)\:=\:\frac{\mathrm{1}}{\mathrm{16}}\:\:, \\ $$$${f}\left(\mathrm{5}\right)\:=\:\frac{\mathrm{1}}{\mathrm{25}}\:\:,\:\:{and}\:\:{f}\left(\mathrm{6}\right)\:=\:\frac{\mathrm{1}}{\mathrm{36}}\:. \\ $$$${Value}\:\:{of}\:\:{f}\left(\mathrm{8}\right)\:=\:? \\ $$
Answered by mr W last updated on 29/Mar/22
![f(8)= [(1,1,1,1,1,1,1),((32),(16),8,4,2,1,(1/4)),((243),(81),(27),9,3,1,(1/9)),((1024),(256),(64),(16),4,1,(1/16)),((3125),(625),(125),(25),5,1,(1/25)),((7776),(1296),(216),(36),6,1,(1/36)),((32768),(4096),(512),(64),8,1,0) ]/ [(1,1,1,1,1,1,0),((32),(16),8,4,2,1,0),((243),(81),(27),9,3,1,0),((1024),(256),(64),(16),4,1,0),((3125),(625),(125),(25),5,1,0),((7776),(1296),(216),(36),6,1,0),((32768),(4096),(512),(64),8,1,(−1)) ] =−((77328)/(34560)) =−((179)/(80))](https://www.tinkutara.com/question/Q167935.png)
$${f}\left(\mathrm{8}\right)=\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}\\{\mathrm{32}}&{\mathrm{16}}&{\mathrm{8}}&{\mathrm{4}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{1}/\mathrm{4}}\\{\mathrm{243}}&{\mathrm{81}}&{\mathrm{27}}&{\mathrm{9}}&{\mathrm{3}}&{\mathrm{1}}&{\mathrm{1}/\mathrm{9}}\\{\mathrm{1024}}&{\mathrm{256}}&{\mathrm{64}}&{\mathrm{16}}&{\mathrm{4}}&{\mathrm{1}}&{\mathrm{1}/\mathrm{16}}\\{\mathrm{3125}}&{\mathrm{625}}&{\mathrm{125}}&{\mathrm{25}}&{\mathrm{5}}&{\mathrm{1}}&{\mathrm{1}/\mathrm{25}}\\{\mathrm{7776}}&{\mathrm{1296}}&{\mathrm{216}}&{\mathrm{36}}&{\mathrm{6}}&{\mathrm{1}}&{\mathrm{1}/\mathrm{36}}\\{\mathrm{32768}}&{\mathrm{4096}}&{\mathrm{512}}&{\mathrm{64}}&{\mathrm{8}}&{\mathrm{1}}&{\mathrm{0}}\end{bmatrix}/\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{32}}&{\mathrm{16}}&{\mathrm{8}}&{\mathrm{4}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{243}}&{\mathrm{81}}&{\mathrm{27}}&{\mathrm{9}}&{\mathrm{3}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{1024}}&{\mathrm{256}}&{\mathrm{64}}&{\mathrm{16}}&{\mathrm{4}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{3125}}&{\mathrm{625}}&{\mathrm{125}}&{\mathrm{25}}&{\mathrm{5}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{7776}}&{\mathrm{1296}}&{\mathrm{216}}&{\mathrm{36}}&{\mathrm{6}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{32768}}&{\mathrm{4096}}&{\mathrm{512}}&{\mathrm{64}}&{\mathrm{8}}&{\mathrm{1}}&{−\mathrm{1}}\end{bmatrix} \\ $$$$=−\frac{\mathrm{77328}}{\mathrm{34560}} \\ $$$$=−\frac{\mathrm{179}}{\mathrm{80}} \\ $$
Commented by naka3546 last updated on 29/Mar/22
$$\mathrm{Thank}\:\:\mathrm{you},\:\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 30/Mar/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{rule}\:\mathrm{to}\:\mathrm{set}\:\mathrm{the}\:\mathrm{matrix}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by mr W last updated on 30/Mar/22
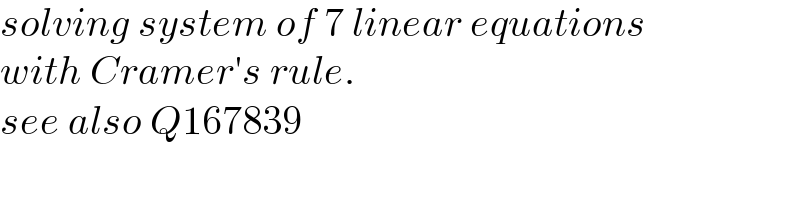
$${solving}\:{system}\:{of}\:\mathrm{7}\:{linear}\:{equations} \\ $$$${with}\:{Cramer}'{s}\:{rule}. \\ $$$${see}\:{also}\:{Q}\mathrm{167839} \\ $$
Commented by mr W last updated on 30/Mar/22
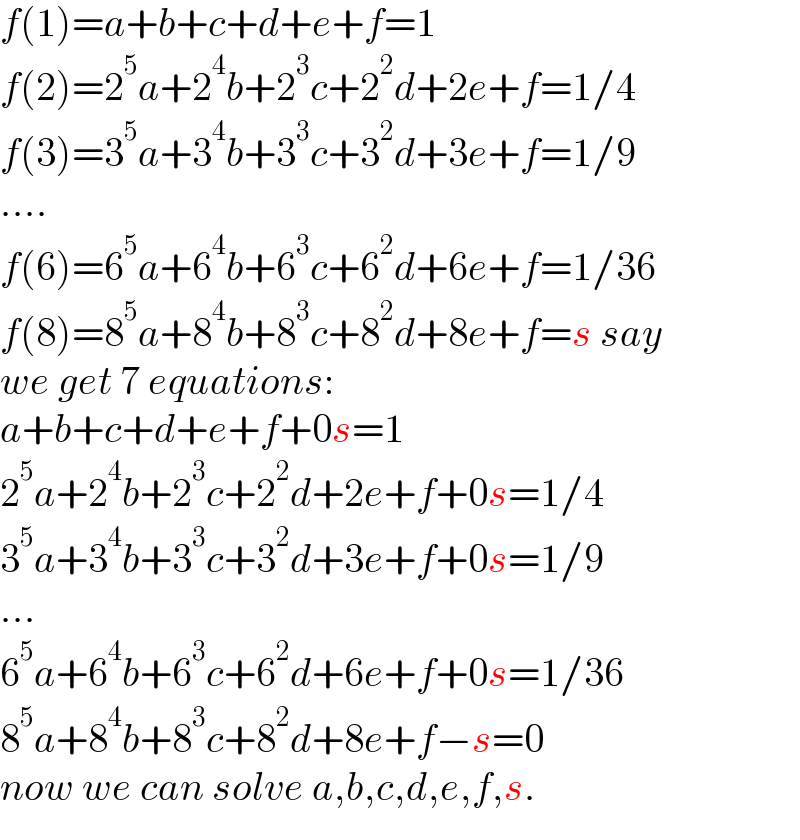
$${f}\left(\mathrm{1}\right)={a}+{b}+{c}+{d}+{e}+{f}=\mathrm{1} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{2}^{\mathrm{5}} {a}+\mathrm{2}^{\mathrm{4}} {b}+\mathrm{2}^{\mathrm{3}} {c}+\mathrm{2}^{\mathrm{2}} {d}+\mathrm{2}{e}+{f}=\mathrm{1}/\mathrm{4} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{3}^{\mathrm{5}} {a}+\mathrm{3}^{\mathrm{4}} {b}+\mathrm{3}^{\mathrm{3}} {c}+\mathrm{3}^{\mathrm{2}} {d}+\mathrm{3}{e}+{f}=\mathrm{1}/\mathrm{9} \\ $$$$…. \\ $$$${f}\left(\mathrm{6}\right)=\mathrm{6}^{\mathrm{5}} {a}+\mathrm{6}^{\mathrm{4}} {b}+\mathrm{6}^{\mathrm{3}} {c}+\mathrm{6}^{\mathrm{2}} {d}+\mathrm{6}{e}+{f}=\mathrm{1}/\mathrm{36} \\ $$$${f}\left(\mathrm{8}\right)=\mathrm{8}^{\mathrm{5}} {a}+\mathrm{8}^{\mathrm{4}} {b}+\mathrm{8}^{\mathrm{3}} {c}+\mathrm{8}^{\mathrm{2}} {d}+\mathrm{8}{e}+{f}={s}\:{say} \\ $$$${we}\:{get}\:\mathrm{7}\:{equations}: \\ $$$${a}+{b}+{c}+{d}+{e}+{f}+\mathrm{0}{s}=\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{5}} {a}+\mathrm{2}^{\mathrm{4}} {b}+\mathrm{2}^{\mathrm{3}} {c}+\mathrm{2}^{\mathrm{2}} {d}+\mathrm{2}{e}+{f}+\mathrm{0}{s}=\mathrm{1}/\mathrm{4} \\ $$$$\mathrm{3}^{\mathrm{5}} {a}+\mathrm{3}^{\mathrm{4}} {b}+\mathrm{3}^{\mathrm{3}} {c}+\mathrm{3}^{\mathrm{2}} {d}+\mathrm{3}{e}+{f}+\mathrm{0}{s}=\mathrm{1}/\mathrm{9} \\ $$$$… \\ $$$$\mathrm{6}^{\mathrm{5}} {a}+\mathrm{6}^{\mathrm{4}} {b}+\mathrm{6}^{\mathrm{3}} {c}+\mathrm{6}^{\mathrm{2}} {d}+\mathrm{6}{e}+{f}+\mathrm{0}{s}=\mathrm{1}/\mathrm{36} \\ $$$$\mathrm{8}^{\mathrm{5}} {a}+\mathrm{8}^{\mathrm{4}} {b}+\mathrm{8}^{\mathrm{3}} {c}+\mathrm{8}^{\mathrm{2}} {d}+\mathrm{8}{e}+{f}−{s}=\mathrm{0} \\ $$$${now}\:{we}\:{can}\:{solve}\:{a},{b},{c},{d},{e},{f},{s}. \\ $$
Commented by Tawa11 last updated on 30/Mar/22
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
