Question Number 91635 by john santu last updated on 02/May/20
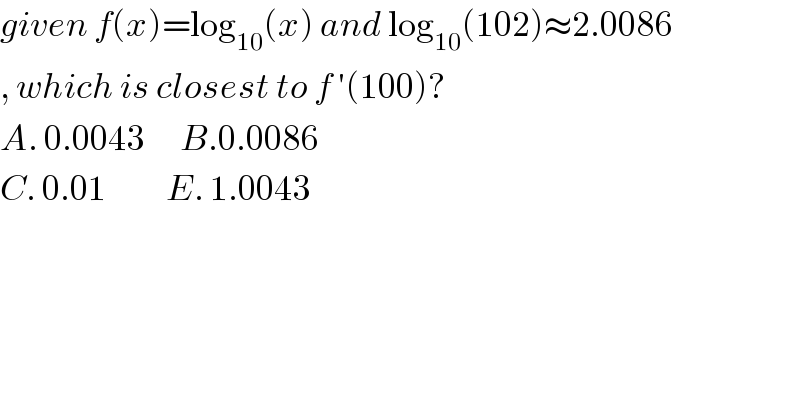
$${given}\:{f}\left({x}\right)=\mathrm{log}_{\mathrm{10}} \left({x}\right)\:{and}\:\mathrm{log}_{\mathrm{10}} \left(\mathrm{102}\right)\approx\mathrm{2}.\mathrm{0086} \\ $$$$,\:{which}\:{is}\:{closest}\:{to}\:{f}\:'\left(\mathrm{100}\right)? \\ $$$${A}.\:\mathrm{0}.\mathrm{0043}\:\:\:\:\:\:{B}.\mathrm{0}.\mathrm{0086} \\ $$$${C}.\:\mathrm{0}.\mathrm{01}\:\:\:\:\:\:\:\:\:\:{E}.\:\mathrm{1}.\mathrm{0043} \\ $$
Commented by mr W last updated on 02/May/20

$${f}\:'\left({x}\right)=\frac{{dy}}{{dx}}\approx\frac{\Delta{y}}{\Delta{x}} \\ $$$${f}\:'\left(\mathrm{100}\right)\approx\frac{{f}\left(\mathrm{102}\right)−{f}\left(\mathrm{100}\right)}{\mathrm{102}−\mathrm{100}}\approx\frac{\mathrm{2}.\mathrm{0086}−\mathrm{2}}{\mathrm{2}}=\mathrm{0}.\mathrm{0043} \\ $$$$\Rightarrow{answer}\:{A} \\ $$
Commented by john santu last updated on 02/May/20

$${yes}… \\ $$
