Question Number 157611 by naka3546 last updated on 25/Oct/21
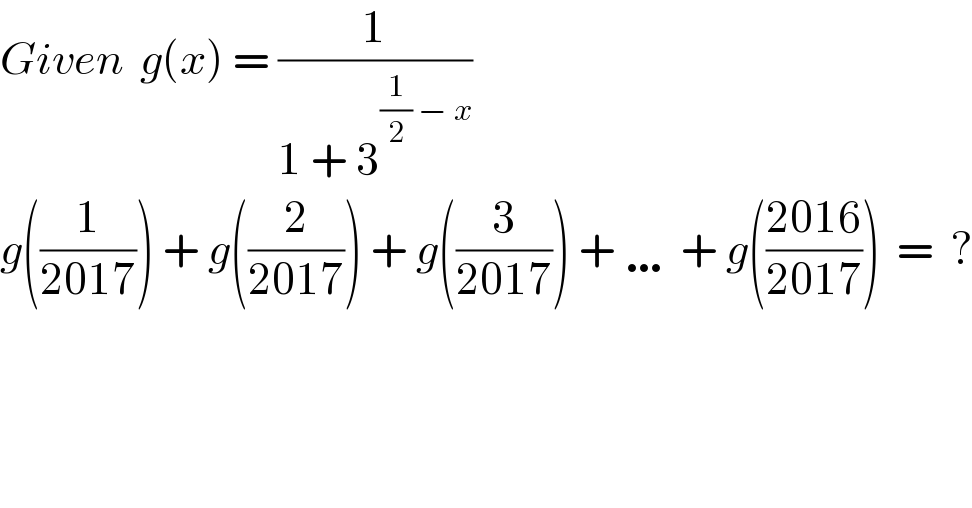
$${Given}\:\:{g}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}\:−\:{x}} } \\ $$$${g}\left(\frac{\mathrm{1}}{\mathrm{2017}}\right)\:+\:{g}\left(\frac{\mathrm{2}}{\mathrm{2017}}\right)\:+\:{g}\left(\frac{\mathrm{3}}{\mathrm{2017}}\right)\:+\:\ldots\:+\:{g}\left(\frac{\mathrm{2016}}{\mathrm{2017}}\right)\:\:=\:\:? \\ $$
Answered by Ar Brandon last updated on 25/Oct/21
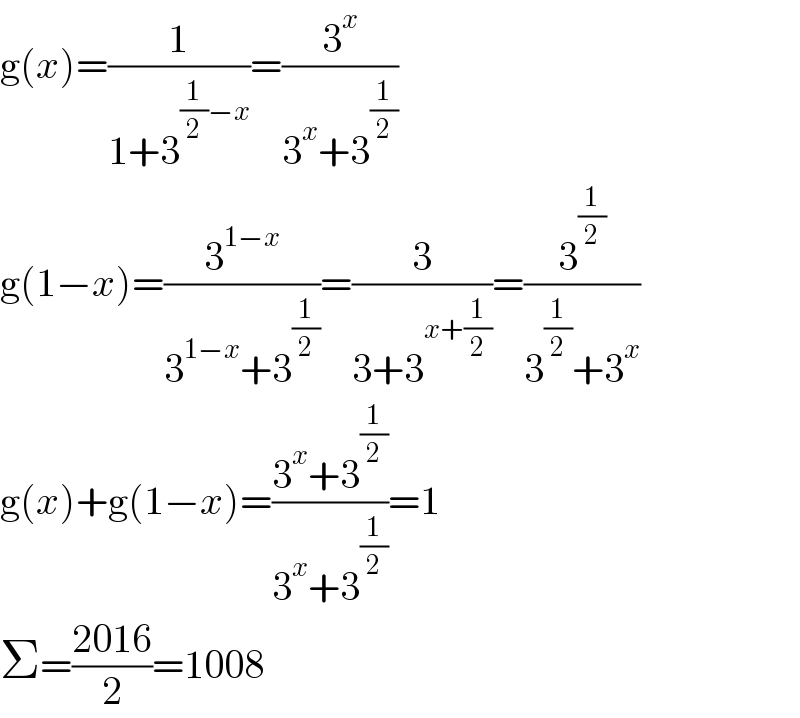
$$\mathrm{g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}−{x}} }=\frac{\mathrm{3}^{{x}} }{\mathrm{3}^{{x}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\mathrm{g}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{3}^{\mathrm{1}−{x}} }{\mathrm{3}^{\mathrm{1}−{x}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\mathrm{3}}{\mathrm{3}+\mathrm{3}^{{x}+\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{3}^{{x}} } \\ $$$$\mathrm{g}\left({x}\right)+\mathrm{g}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{3}^{{x}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{3}^{{x}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} }=\mathrm{1} \\ $$$$\Sigma=\frac{\mathrm{2016}}{\mathrm{2}}=\mathrm{1008} \\ $$
Commented by naka3546 last updated on 25/Oct/21
$${Thank}\:\:{you},\:\:{sir}. \\ $$
