Menu Close

Given-lim-x-5-f-x-a-x-5-8-lim-x-5-x-2-ax-b-f-x-a-1-find-the-value-of-b-23-

Tinku Tara 0 Comments
Pin




Question Number 105383 by bemath last updated on 28/Jul/20
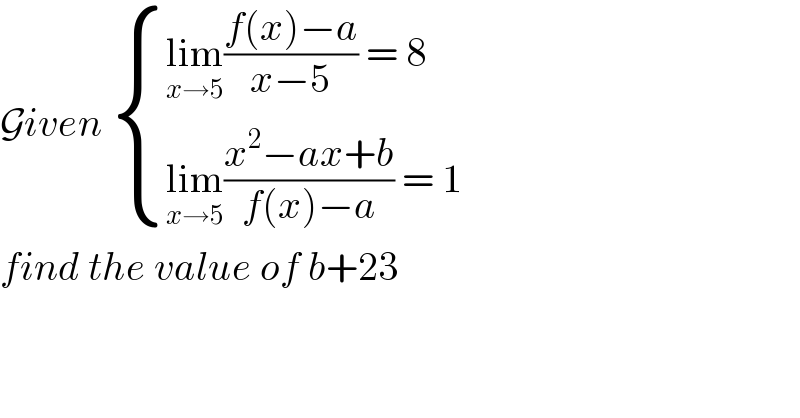
Given { ((lim_(x→5) ((f(x)−a)/(x−5)) = 8)),((lim_(x→5) ((x^2 −ax+b)/(f(x)−a)) = 1)) :} find the value of b+23
Given{limx→5f(x)−ax−5=8limx→5x2−ax+bf(x)−a=1findthevalueofb+23
Answered by john santu last updated on 28/Jul/20
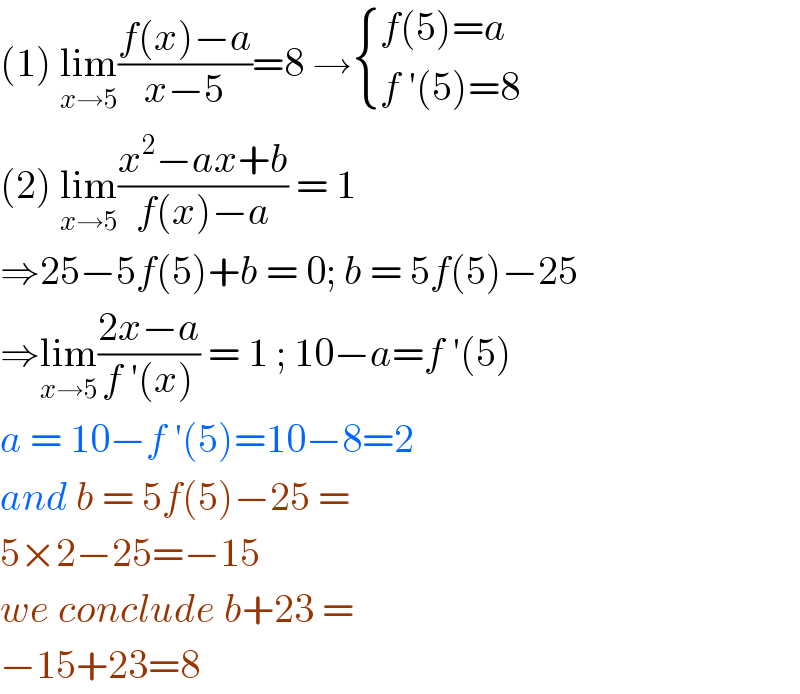
(1) lim_(x→5) ((f(x)−a)/(x−5))=8 → { ((f(5)=a)),((f ′(5)=8)) :} (2) lim_(x→5) ((x^2 −ax+b)/(f(x)−a)) = 1 ⇒25−5f(5)+b = 0; b = 5f(5)−25 ⇒lim_(x→5) ((2x−a)/(f ′(x))) = 1 ; 10−a=f ′(5) a = 10−f ′(5)=10−8=2 and b = 5f(5)−25 = 5×2−25=−15 we conclude b+23 = −15+23=8
(1)limx→5f(x)−ax−5=8→{f(5)=af′(5)=8(2)limx→5x2−ax+bf(x)−a=1⇒25−5f(5)+b=0;b=5f(5)−25⇒limx→52x−af′(x)=1;10−a=f′(5)a=10−f′(5)=10−8=2andb=5f(5)−25=5×2−25=−15weconcludeb+23=−15+23=8
Commented by bemath last updated on 28/Jul/20
jooss
jooss

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *