Question Number 112505 by bemath last updated on 08/Sep/20
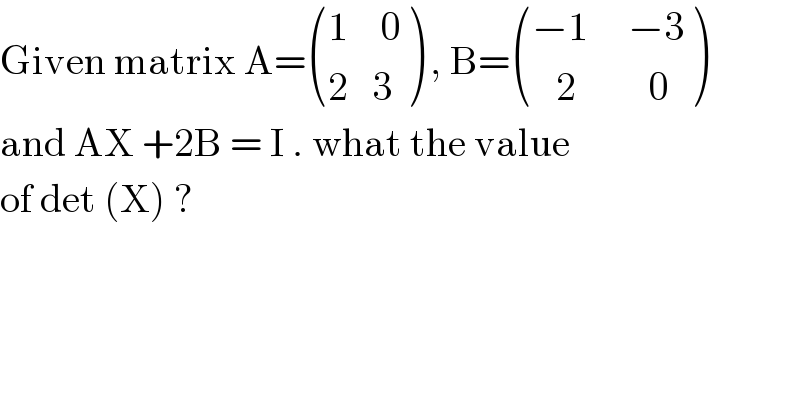
$$\mathrm{Given}\:\mathrm{matrix}\:\mathrm{A}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{0}}\\{\mathrm{2}\:\:\:\mathrm{3}}\end{pmatrix}\:,\:\mathrm{B}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:−\mathrm{3}}\\{\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{and}\:\mathrm{AX}\:+\mathrm{2B}\:=\:\mathrm{I}\:.\:\mathrm{what}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{det}\:\left(\mathrm{X}\right)\:? \\ $$
Answered by john santu last updated on 08/Sep/20
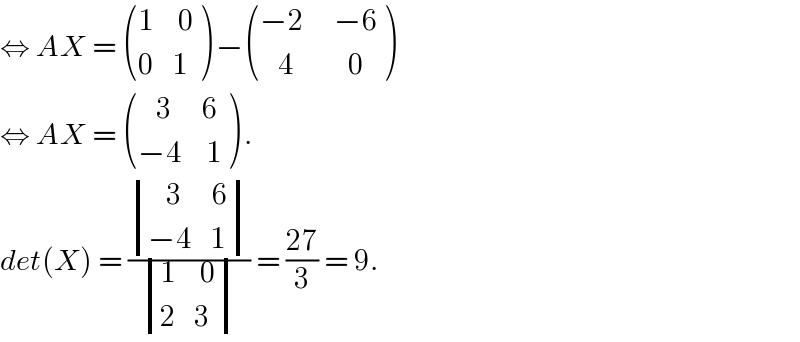
$$\Leftrightarrow\:{AX}\:=\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\:−\begin{pmatrix}{−\mathrm{2}\:\:\:\:\:−\mathrm{6}}\\{\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$\Leftrightarrow\:{AX}\:=\:\begin{pmatrix}{\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{6}}\\{−\mathrm{4}\:\:\:\:\mathrm{1}}\end{pmatrix}\:. \\ $$$${det}\left({X}\right)\:=\:\frac{\begin{vmatrix}{\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{6}}\\{−\mathrm{4}\:\:\:\mathrm{1}}\end{vmatrix}}{\begin{vmatrix}{\mathrm{1}\:\:\:\:\mathrm{0}}\\{\mathrm{2}\:\:\:\mathrm{3}}\end{vmatrix}}\:=\:\frac{\mathrm{27}}{\mathrm{3}}\:=\:\mathrm{9}. \\ $$
