Question Number 115520 by bemath last updated on 26/Sep/20

$${Given}\:{matrix}\:{A}\:=\:\begin{pmatrix}{{a}\:\:\:\mathrm{1}\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:{a}\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\mathrm{1}\:\:\:\:{a}}\end{pmatrix}\: \\ $$$${If}\:{B}\:=\:{b}.{A}\:{and}\:{B}\:{is}\:{orthogonal}\: \\ $$$${determine}\:{value}\:{of}\:{a}\:{and}\:{b}. \\ $$
Answered by bobhans last updated on 26/Sep/20
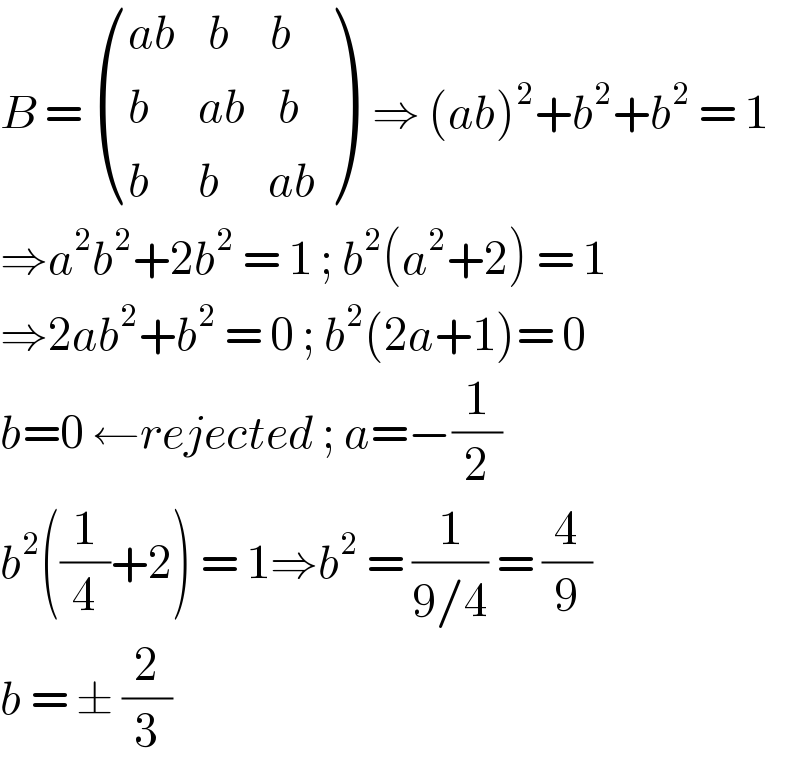
$${B}\:=\:\begin{pmatrix}{{ab}\:\:\:\:{b}\:\:\:\:\:{b}}\\{{b}\:\:\:\:\:\:{ab}\:\:\:\:{b}}\\{{b}\:\:\:\:\:\:{b}\:\:\:\:\:\:{ab}}\end{pmatrix}\:\:\Rightarrow\:\left({ab}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} +{b}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} \:=\:\mathrm{1}\:;\:{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{2}\right)\:=\:\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{ab}^{\mathrm{2}} +{b}^{\mathrm{2}} \:=\:\mathrm{0}\:;\:{b}^{\mathrm{2}} \left(\mathrm{2}{a}+\mathrm{1}\right)=\:\mathrm{0} \\ $$$${b}=\mathrm{0}\:\leftarrow{rejected}\:;\:{a}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}\right)\:=\:\mathrm{1}\Rightarrow{b}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{9}/\mathrm{4}}\:=\:\frac{\mathrm{4}}{\mathrm{9}} \\ $$$${b}\:=\:\pm\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by bemath last updated on 26/Sep/20

$${greattt} \\ $$
