Question Number 97637 by Ar Brandon last updated on 09/Jun/20
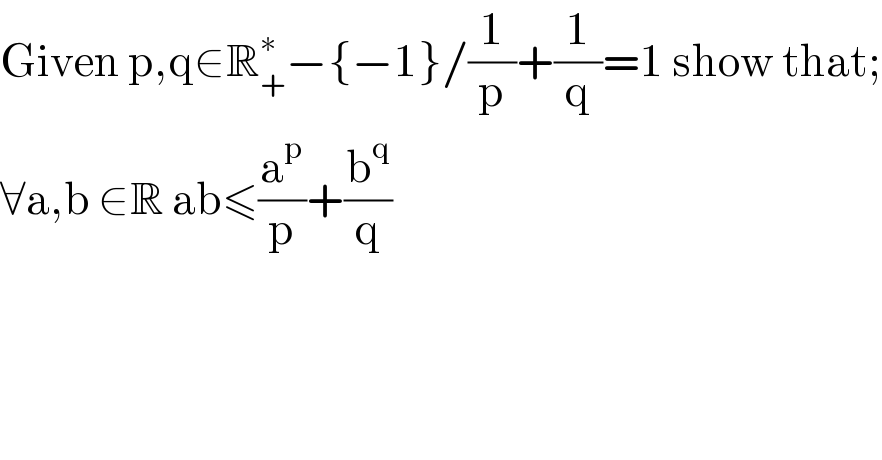
$$\mathrm{Given}\:\mathrm{p},\mathrm{q}\in\mathbb{R}_{+} ^{\ast} −\left\{−\mathrm{1}\right\}/\frac{\mathrm{1}}{\mathrm{p}}+\frac{\mathrm{1}}{\mathrm{q}}=\mathrm{1}\:\mathrm{show}\:\mathrm{that}; \\ $$$$\forall\mathrm{a},\mathrm{b}\:\in\mathbb{R}\:\mathrm{ab}\leqslant\frac{\mathrm{a}^{\mathrm{p}} }{\mathrm{p}}+\frac{\mathrm{b}^{\mathrm{q}} }{\mathrm{q}} \\ $$
Commented by arcana last updated on 09/Jun/20

$$\mathrm{its}\:\mathrm{the}\:\mathrm{Young}'\mathrm{s}\:\mathrm{inequality}.\:\mathrm{You}\:\mathrm{can} \\ $$$$\mathrm{find}\:\mathrm{it}\:\mathrm{in}\:\mathrm{various}\:\mathrm{web}\:\mathrm{pages} \\ $$
