Question Number 116493 by bemath last updated on 04/Oct/20
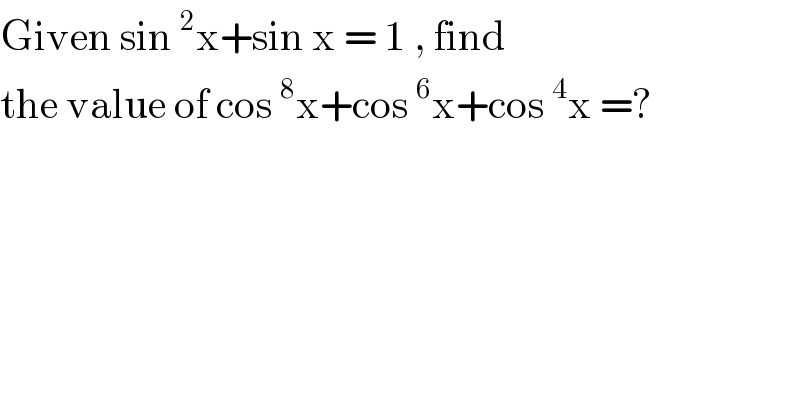
$$\mathrm{Given}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{1}\:,\:\mathrm{find}\: \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{cos}\:^{\mathrm{8}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{6}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\:=? \\ $$
Answered by bobhans last updated on 04/Oct/20
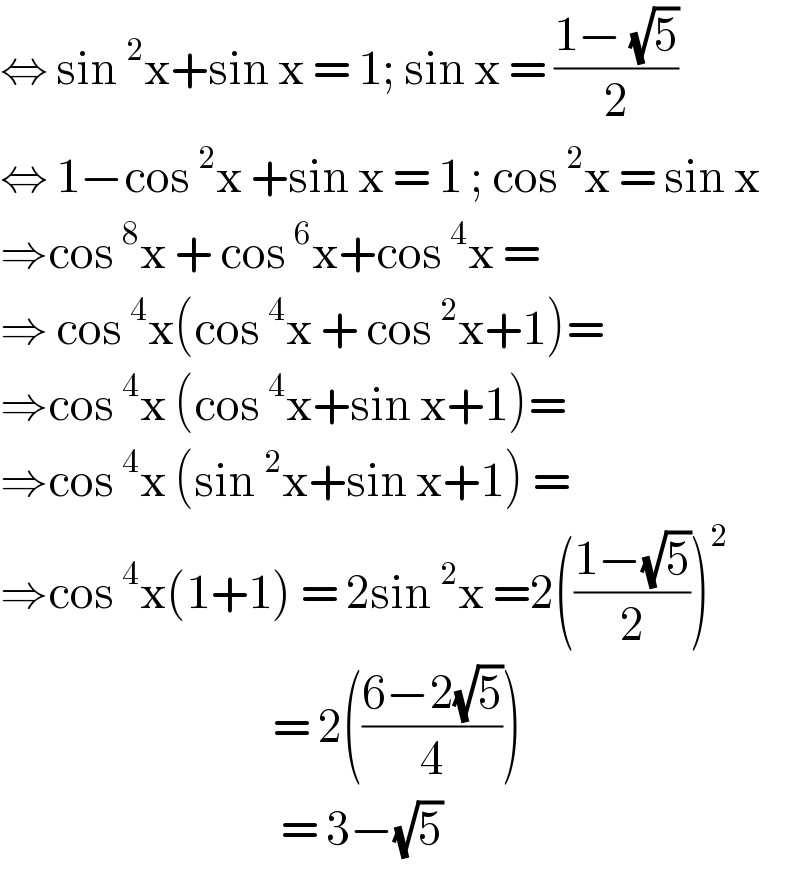
$$\Leftrightarrow\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{1};\:\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{1}−\:\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:+\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{1}\:;\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{sin}\:\mathrm{x} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{8}} \mathrm{x}\:+\:\mathrm{cos}\:^{\mathrm{6}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\:=\: \\ $$$$\Rightarrow\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\left(\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\:+\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)= \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\:\left(\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}+\mathrm{sin}\:\mathrm{x}+\mathrm{1}\right)= \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\:\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:\mathrm{x}+\mathrm{1}\right)\:= \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\left(\mathrm{1}+\mathrm{1}\right)\:=\:\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\:=\mathrm{2}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{3}−\sqrt{\mathrm{5}} \\ $$
Answered by som(math1967) last updated on 04/Oct/20
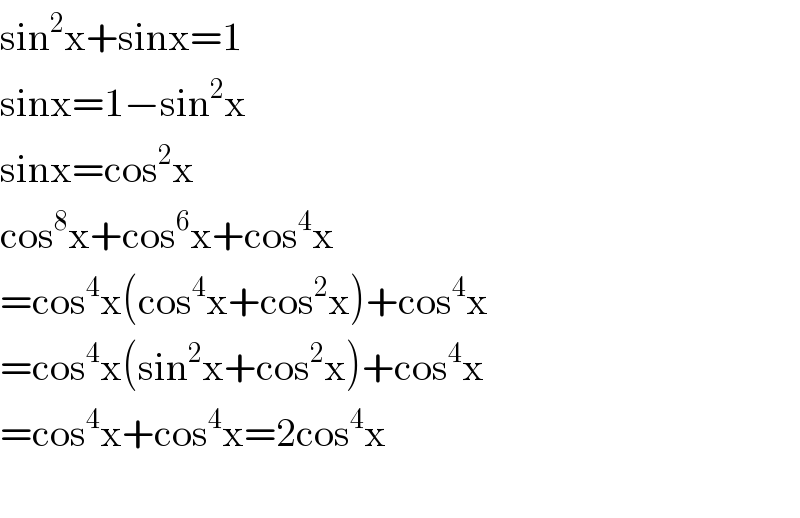
$$\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{sinx}=\mathrm{1} \\ $$$$\mathrm{sinx}=\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{sinx}=\mathrm{cos}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{cos}^{\mathrm{8}} \mathrm{x}+\mathrm{cos}^{\mathrm{6}} \mathrm{x}+\mathrm{cos}^{\mathrm{4}} \mathrm{x} \\ $$$$=\mathrm{cos}^{\mathrm{4}} \mathrm{x}\left(\mathrm{cos}^{\mathrm{4}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{cos}^{\mathrm{4}} \mathrm{x} \\ $$$$=\mathrm{cos}^{\mathrm{4}} \mathrm{x}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)+\mathrm{cos}^{\mathrm{4}} \mathrm{x} \\ $$$$=\mathrm{cos}^{\mathrm{4}} \mathrm{x}+\mathrm{cos}^{\mathrm{4}} \mathrm{x}=\mathrm{2cos}^{\mathrm{4}} \mathrm{x} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 04/Oct/20
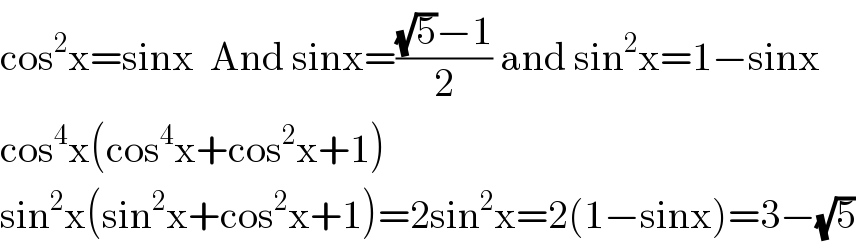
$$\mathrm{cos}^{\mathrm{2}} \mathrm{x}=\mathrm{sinx}\:\:\mathrm{And}\:\mathrm{sinx}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}=\mathrm{1}−\mathrm{sinx} \\ $$$$\mathrm{cos}^{\mathrm{4}} \mathrm{x}\left(\mathrm{cos}^{\mathrm{4}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right) \\ $$$$\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)=\mathrm{2sin}^{\mathrm{2}} \mathrm{x}=\mathrm{2}\left(\mathrm{1}−\mathrm{sinx}\right)=\mathrm{3}−\sqrt{\mathrm{5}} \\ $$
