Question Number 176581 by cortano1 last updated on 22/Sep/22

$$\:\:\mathrm{Given}\:\begin{cases}{\mathrm{sin}\:\mathrm{a}+\mathrm{sin}\:\mathrm{b}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\\{\mathrm{cos}\:\mathrm{a}+\mathrm{cos}\:\mathrm{b}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}}\end{cases} \\ $$$$\:\mathrm{for}\:\mathrm{a},\mathrm{b}\:\mathrm{real}\:\mathrm{numbers}.\:\mathrm{Evaluate} \\ $$$$\:\mathrm{sin}\:\left(\mathrm{a}+\mathrm{b}\right). \\ $$$$\:\left(\mathrm{A}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\left(\mathrm{B}\right)\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\:\:\:\:\left(\mathrm{E}\right)−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\:\:\left(\mathrm{C}\right)\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$
Answered by som(math1967) last updated on 22/Sep/22
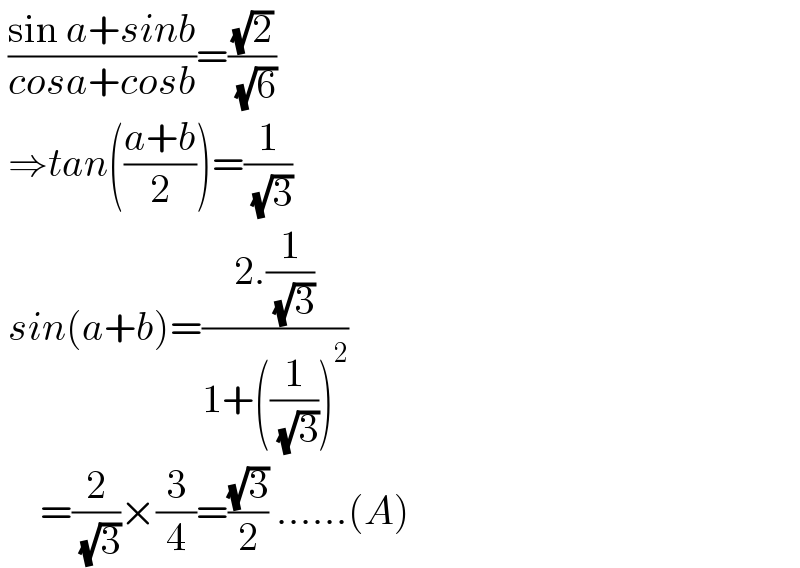
$$\:\frac{\mathrm{sin}\:{a}+{sinb}}{{cosa}+{cosb}}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{6}}} \\ $$$$\:\Rightarrow{tan}\left(\frac{{a}+{b}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\:{sin}\left({a}+{b}\right)=\frac{\mathrm{2}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}×\frac{\mathrm{3}}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:……\left({A}\right) \\ $$
