Question Number 128681 by bemath last updated on 09/Jan/21
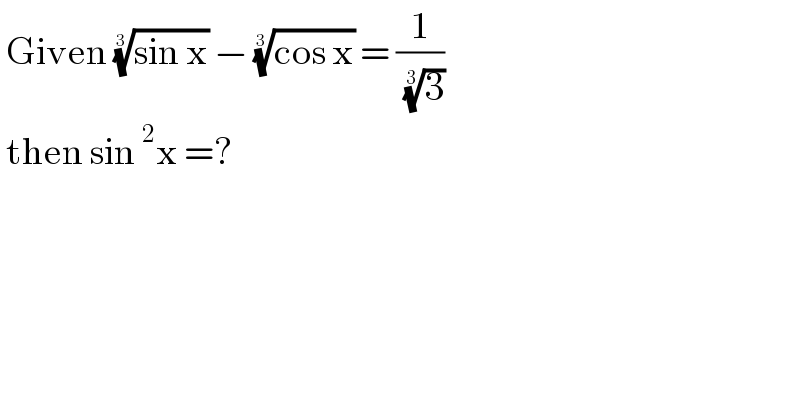
$$\:\mathrm{Given}\:\sqrt[{\mathrm{3}}]{\mathrm{sin}\:\mathrm{x}}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{cos}\:\mathrm{x}}\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}} \\ $$$$\:\mathrm{then}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:=?\: \\ $$
Commented by MJS_new last updated on 09/Jan/21
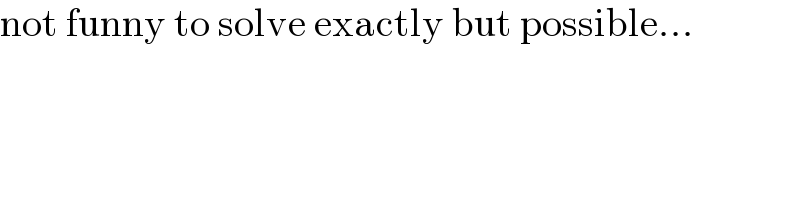
$$\mathrm{not}\:\mathrm{funny}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{exactly}\:\mathrm{but}\:\mathrm{possible}… \\ $$
Answered by MJS_new last updated on 09/Jan/21
![(a)^(1/3) −(b)^(1/3) =(c)^(1/3) ∣^3 a−b−3((ab))^(1/3) ((a)^(1/3) −(b)^(1/3) )=c [insert from above (a)^(1/3) −(b)^(1/3) =(c)^(1/3) ] 3((abc))^(1/3) =a−b−c 27abc=(a+b−c)^3 a=sin x ∧b=cos x ∧ c=(1/3) 9sin x cos x =(−(1/3)+sin x −cos x)^3 let t=tan (x/2) ⇔ x=2arctan t and transforming t^6 +((279)/4)t^5 +21t^4 −9t^3 −42t^2 −((99)/4)t−8=0 amazingly this can be completely solved I get 3 square factors f_1 (t)f_2 (t)f_3 (t)=0 f_1 (t)=t^2 +(3/4)t+(1/4) f_2 (t)=t^2 +((3(23−3(√(57))))/2)t−((67−9(√(57)))/2) f_3 (t)=t^2 +((3(23+3(√(57))))/2)t−((67+9(√(57)))/2) only f_3 (t)=0 has real roots t_1 =−((3(23+3(√(57)))+(√(2(4957+657(√(57)))))/4)≈−69.4459 t_2 =−((3(23+3(√(57)))−(√(2(4957+657(√(57)))))/4)≈.971609 sin^2 x =(((2t)/(t^2 +1)))^2 now the rest is easy](https://www.tinkutara.com/question/Q128726.png)
$$\sqrt[{\mathrm{3}}]{{a}}−\sqrt[{\mathrm{3}}]{{b}}=\sqrt[{\mathrm{3}}]{{c}}\:\:\:\:\:\mid^{\mathrm{3}} \\ $$$${a}−{b}−\mathrm{3}\sqrt[{\mathrm{3}}]{{ab}}\left(\sqrt[{\mathrm{3}}]{{a}}−\sqrt[{\mathrm{3}}]{{b}}\right)={c} \\ $$$$\:\:\:\:\:\left[\mathrm{insert}\:\mathrm{from}\:\mathrm{above}\:\sqrt[{\mathrm{3}}]{{a}}−\sqrt[{\mathrm{3}}]{{b}}=\sqrt[{\mathrm{3}}]{{c}}\right] \\ $$$$\mathrm{3}\sqrt[{\mathrm{3}}]{{abc}}={a}−{b}−{c} \\ $$$$\mathrm{27}{abc}=\left({a}+{b}−{c}\right)^{\mathrm{3}} \\ $$$${a}=\mathrm{sin}\:{x}\:\wedge{b}=\mathrm{cos}\:{x}\:\wedge\:{c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{9sin}\:{x}\:\mathrm{cos}\:{x}\:=\left(−\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\right)^{\mathrm{3}} \\ $$$$\mathrm{let}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Leftrightarrow\:{x}=\mathrm{2arctan}\:{t}\:\mathrm{and}\:\mathrm{transforming} \\ $$$${t}^{\mathrm{6}} +\frac{\mathrm{279}}{\mathrm{4}}{t}^{\mathrm{5}} +\mathrm{21}{t}^{\mathrm{4}} −\mathrm{9}{t}^{\mathrm{3}} −\mathrm{42}{t}^{\mathrm{2}} −\frac{\mathrm{99}}{\mathrm{4}}{t}−\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{amazingly}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{completely}\:\mathrm{solved} \\ $$$$\mathrm{I}\:\mathrm{get}\:\mathrm{3}\:\mathrm{square}\:\mathrm{factors} \\ $$$${f}_{\mathrm{1}} \left({t}\right){f}_{\mathrm{2}} \left({t}\right){f}_{\mathrm{3}} \left({t}\right)=\mathrm{0} \\ $$$${f}_{\mathrm{1}} \left({t}\right)={t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{t}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${f}_{\mathrm{2}} \left({t}\right)={t}^{\mathrm{2}} +\frac{\mathrm{3}\left(\mathrm{23}−\mathrm{3}\sqrt{\mathrm{57}}\right)}{\mathrm{2}}{t}−\frac{\mathrm{67}−\mathrm{9}\sqrt{\mathrm{57}}}{\mathrm{2}} \\ $$$${f}_{\mathrm{3}} \left({t}\right)={t}^{\mathrm{2}} +\frac{\mathrm{3}\left(\mathrm{23}+\mathrm{3}\sqrt{\mathrm{57}}\right)}{\mathrm{2}}{t}−\frac{\mathrm{67}+\mathrm{9}\sqrt{\mathrm{57}}}{\mathrm{2}} \\ $$$$\mathrm{only}\:{f}_{\mathrm{3}} \left({t}\right)=\mathrm{0}\:\mathrm{has}\:\mathrm{real}\:\mathrm{roots} \\ $$$${t}_{\mathrm{1}} =−\frac{\mathrm{3}\left(\mathrm{23}+\mathrm{3}\sqrt{\mathrm{57}}\right)+\sqrt{\mathrm{2}\left(\mathrm{4957}+\mathrm{657}\sqrt{\mathrm{57}}\right.}}{\mathrm{4}}\approx−\mathrm{69}.\mathrm{4459} \\ $$$${t}_{\mathrm{2}} =−\frac{\mathrm{3}\left(\mathrm{23}+\mathrm{3}\sqrt{\mathrm{57}}\right)−\sqrt{\mathrm{2}\left(\mathrm{4957}+\mathrm{657}\sqrt{\mathrm{57}}\right.}}{\mathrm{4}}\approx.\mathrm{971609} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}\:=\left(\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Commented by bemath last updated on 10/Jan/21
������
