Question Number 129181 by liberty last updated on 13/Jan/21
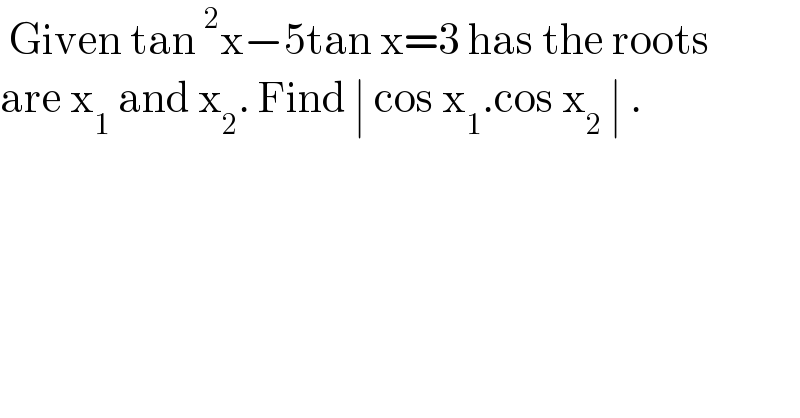
$$\:\mathrm{Given}\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{5tan}\:\mathrm{x}=\mathrm{3}\:\mathrm{has}\:\mathrm{the}\:\mathrm{roots}\: \\ $$$$\mathrm{are}\:\mathrm{x}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} .\:\mathrm{Find}\:\mid\:\mathrm{cos}\:\mathrm{x}_{\mathrm{1}} .\mathrm{cos}\:\mathrm{x}_{\mathrm{2}} \:\mid\:. \\ $$
Commented by MJS_new last updated on 13/Jan/21
$$\mathrm{see}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{question}\:\mathrm{128995} \\ $$
Answered by bramlexs22 last updated on 13/Jan/21

$$\:\mathrm{Consider}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{and}\:\mathrm{product}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{5tan}\:\mathrm{x}−\mathrm{3}\:=\:\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{tan}\:\mathrm{x}_{\mathrm{1}} +\mathrm{tan}\:\mathrm{x}_{\mathrm{2}} \:=\:\mathrm{5}}\\{\mathrm{tan}\:\mathrm{x}_{\mathrm{1}} .\mathrm{tan}\:\mathrm{x}_{\mathrm{2}} \:=\:−\mathrm{3}}\end{cases} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{tan}\:\left(\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} \right)=\frac{\mathrm{5}}{\mathrm{1}−\left(−\mathrm{3}\right)}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{and}\:\mathrm{sin}\:\left(\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} \right)\:=\:\pm\:\frac{\mathrm{5}}{\:\sqrt{\mathrm{41}}} \\ $$$$\mathrm{from}\:\mathrm{tan}\:\mathrm{x}_{\mathrm{1}} +\mathrm{tan}\:\mathrm{x}_{\mathrm{2}} \:=\:\mathrm{5}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\:\mathrm{5cos}\:\mathrm{x}_{\mathrm{1}} .\mathrm{cos}\:\mathrm{x}_{\mathrm{2}} \:=\:\mathrm{sin}\:\left(\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} \right) \\ $$$$\:\mid\:\mathrm{cos}\:\mathrm{x}_{\mathrm{1}} .\mathrm{cos}\:\mathrm{x}_{\mathrm{2}} \:\mid\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{41}}} \\ $$$$\: \\ $$
Commented by liberty last updated on 13/Jan/21

$$\mathrm{nice}… \\ $$
