Question Number 35738 by Rio Mike last updated on 22/May/18

$$\:{Given}\:{that}\:\:\int_{\mathrm{0}} ^{{k}} {x}^{\mathrm{2}} =\:\mathrm{16} \\ $$$${find}\:{the}\:{value}\:{of}\:{k} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/May/18
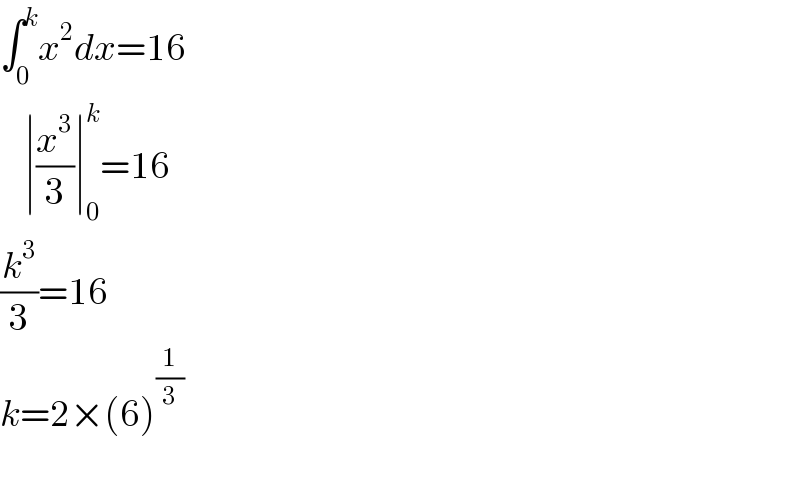
$$\int_{\mathrm{0}} ^{{k}} {x}^{\mathrm{2}} {dx}=\mathrm{16} \\ $$$$\:\:\:\:\mid\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\mid_{\mathrm{0}} ^{{k}} =\mathrm{16} \\ $$$$\frac{{k}^{\mathrm{3}} }{\mathrm{3}}=\mathrm{16} \\ $$$${k}=\mathrm{2}×\left(\mathrm{6}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$ \\ $$
Answered by candre last updated on 22/May/18
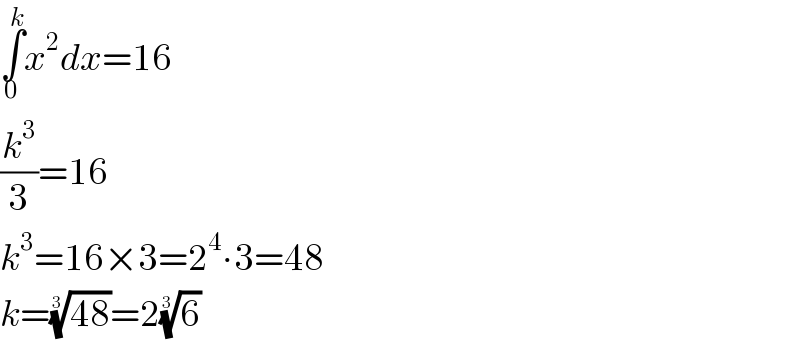
$$\underset{\mathrm{0}} {\overset{{k}} {\int}}{x}^{\mathrm{2}} {dx}=\mathrm{16} \\ $$$$\frac{{k}^{\mathrm{3}} }{\mathrm{3}}=\mathrm{16} \\ $$$${k}^{\mathrm{3}} =\mathrm{16}×\mathrm{3}=\mathrm{2}^{\mathrm{4}} \centerdot\mathrm{3}=\mathrm{48} \\ $$$${k}=\sqrt[{\mathrm{3}}]{\mathrm{48}}=\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{6}} \\ $$
