Given-that-17-27-4-6-1-3-and-17-27-4-6-1-3-are-the-roots-of-the-equation-x-2-ax-b-0-Find-the-value-of-ab-

Question Number 116358 by bemath last updated on 03/Oct/20

Given that \sqrt[3]{17 - \frac{27}{4} \sqrt{6}} and \sqrt[3]{17 + \frac{27}{4} \sqrt{6}}

are the roots of the equation

x^{2} - ax + b = 0 . Find the value of ab .

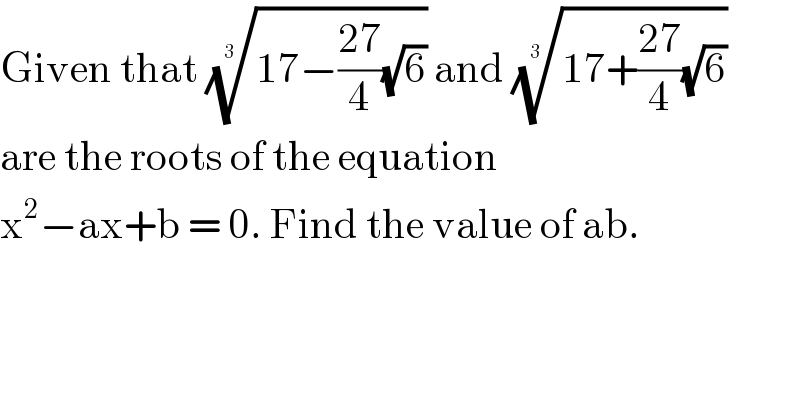
Answered by MJS_new last updated on 03/Oct/20

\sqrt[3]{17 \pm \frac{27 \sqrt{6}}{4}} = 2 \pm \frac{\sqrt{6}}{2}

(x - 2 + \frac{\sqrt{6}}{2}) (x - 2 - \frac{\sqrt{6}}{2}) = x^{2} - 4 x + \frac{5}{2}

\Rightarrow a b = + 10

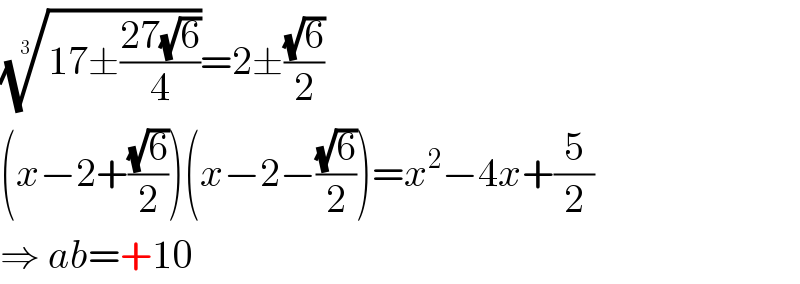
Commented by bemath last updated on 03/Oct/20

typo sir . the equation x^{2} - ax + b = 0

then a = 4 & b = \frac{5}{2} sir

Commented by MJS_new last updated on 03/Oct/20

yes {you}^{'} re right

Commented by bobhans last updated on 03/Oct/20

i like your method prof . {it}^{'} s great

Answered by bobhans last updated on 03/Oct/20

Let x_{1} = \sqrt[3]{17 - \frac{27}{4} \sqrt{6}} and x_{2} = \sqrt[3]{17 + \frac{27}{4} \sqrt{6}}

Then x_{1} . x_{2} = \sqrt[3]{(17 - \frac{27}{4} \sqrt{6}) (17 + \frac{27}{4} \sqrt{6})}

= \sqrt[3]{\frac{125}{8}} = \frac{5}{2}

x_{1} + x_{2} = a \Rightarrow a^{3} = x_{1}^{3} + x_{2}^{3} + 3 x_{1} x_{2} (x_{1} + x_{2})

a^{3} = 34 + 3 a b \Rightarrow a^{3} = 34 + \frac{15}{2} a

\Rightarrow 2 a^{3} - 15 a - 68 = 0

\Rightarrow (a - 4) (2 a^{2} + 8 a + 17) = 0, for a \in R

we get a = 4 and thus a b = 4 \times \frac{5}{2} = 10

Facebook Tweet Pin