Question Number 175961 by pete last updated on 10/Sep/22
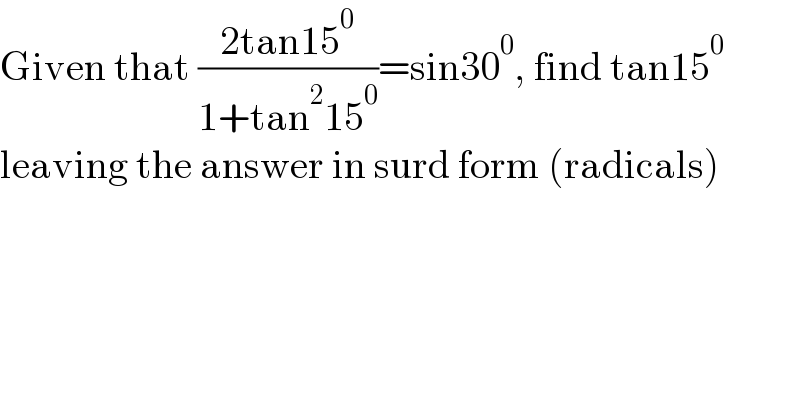
$$\mathrm{Given}\:\mathrm{that}\:\frac{\mathrm{2tan15}^{\mathrm{0}} }{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{15}^{\mathrm{0}} }=\mathrm{sin30}^{\mathrm{0}} ,\:\mathrm{find}\:\mathrm{tan15}^{\mathrm{0}} \\ $$$$\mathrm{leaving}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{surd}\:\mathrm{form}\:\left(\mathrm{radicals}\right) \\ $$
Answered by BaliramKumar last updated on 10/Sep/22

$${let}\:\:\:\:\:\:{tan}\mathrm{15}°\:=\:{x} \\ $$$$\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{1}+{x}^{\mathrm{2}} \:=\:\mathrm{4}{x} \\ $$$${x}^{\mathrm{2}} \:−\:\mathrm{4}{x}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{\mathrm{4}\:\pm\:\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}}\:=\:\frac{\mathrm{4}\:\pm\:\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\mathrm{2}\:\pm\:\sqrt{\mathrm{3}} \\ $$$$\underset{\mathrm{invalid}} {\underbrace{{x}\:=\:\mathrm{2}\:+\:\sqrt{\mathrm{3}}\:=\:\mathrm{3}.\mathrm{732}}}\:\:\:\:\:\:\:\:\:\:\:{x}\:=\:\mathrm{2}\:−\:\sqrt{\mathrm{3}}\:=\:\mathrm{0}.\mathrm{2679} \\ $$$${tan}\mathrm{0}°<{tan}\mathrm{15}°<{tan}\mathrm{45}° \\ $$$$\mathrm{0}<{tan}\mathrm{15}°<\mathrm{1} \\ $$$$\mathrm{0}<\mathrm{0}.\mathrm{2679}<\mathrm{1} \\ $$$$\therefore\:{tan}\mathrm{15}°\:=\:\mathrm{2}\:−\:\sqrt{\mathrm{3}}\:=\:\mathrm{0}.\mathrm{2679} \\ $$
Commented by pete last updated on 10/Sep/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
