Question Number 124595 by physicstutes last updated on 04/Dec/20
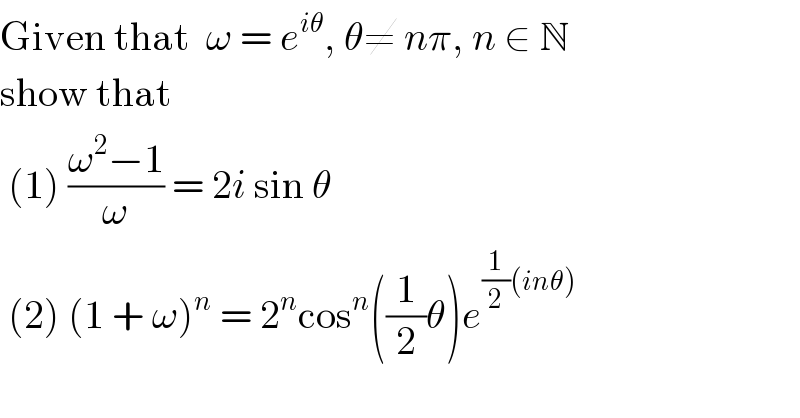
$$\mathrm{Given}\:\mathrm{that}\:\:\omega\:=\:{e}^{{i}\theta} ,\:\theta\neq\:{n}\pi,\:{n}\:\in\:\mathbb{N} \\ $$$$\mathrm{show}\:\mathrm{that}\: \\ $$$$\:\left(\mathrm{1}\right)\:\frac{\omega^{\mathrm{2}} −\mathrm{1}}{\omega}\:=\:\mathrm{2}{i}\:\mathrm{sin}\:\theta \\ $$$$\:\left(\mathrm{2}\right)\:\left(\mathrm{1}\:+\:\omega\right)^{{n}} \:=\:\mathrm{2}^{{n}} \mathrm{cos}^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\theta\right){e}^{\frac{\mathrm{1}}{\mathrm{2}}\left({in}\theta\right)} \\ $$
Answered by Ar Brandon last updated on 04/Dec/20
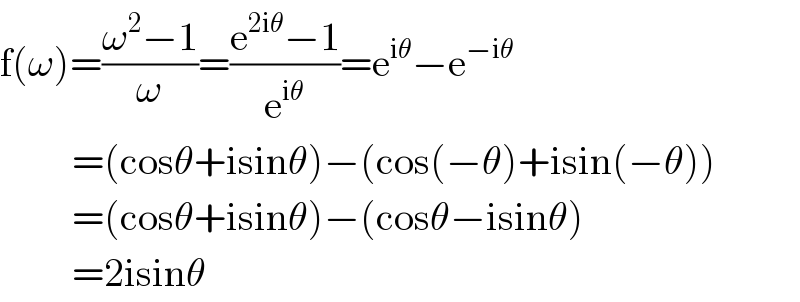
$$\mathrm{f}\left(\omega\right)=\frac{\omega^{\mathrm{2}} −\mathrm{1}}{\omega}=\frac{\mathrm{e}^{\mathrm{2i}\theta} −\mathrm{1}}{\mathrm{e}^{\mathrm{i}\theta} }=\mathrm{e}^{\mathrm{i}\theta} −\mathrm{e}^{−\mathrm{i}\theta} \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{cos}\theta+\mathrm{isin}\theta\right)−\left(\mathrm{cos}\left(−\theta\right)+\mathrm{isin}\left(−\theta\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{cos}\theta+\mathrm{isin}\theta\right)−\left(\mathrm{cos}\theta−\mathrm{isin}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2isin}\theta \\ $$
Commented by physicstutes last updated on 04/Dec/20

$$\mathrm{thats}\:\mathrm{great} \\ $$
Answered by mnjuly1970 last updated on 04/Dec/20
![1:ω^2 −1=(cos(2θ)+isin(2θ))−1=2isin(θ)cos(θ)−2sin^2 (θ) =2isin(θ)[cos(θ)+isin(θ)] ⇒((ω^2 −1)/ω)=2isin(θ) corallary :Ω=∫_0 ^(π/2) ln(Im(((ω^2 −1)/(2w))))dθ=−(π/2)ln(2)✓](https://www.tinkutara.com/question/Q124598.png)
$$\mathrm{1}:\omega^{\mathrm{2}} −\mathrm{1}=\left({cos}\left(\mathrm{2}\theta\right)+{isin}\left(\mathrm{2}\theta\right)\right)−\mathrm{1}=\mathrm{2}{isin}\left(\theta\right){cos}\left(\theta\right)−\mathrm{2}{sin}^{\mathrm{2}} \left(\theta\right) \\ $$$$\:\:\:=\mathrm{2}{isin}\left(\theta\right)\left[{cos}\left(\theta\right)+{isin}\left(\theta\right)\right] \\ $$$$\:\Rightarrow\frac{\omega^{\mathrm{2}} −\mathrm{1}}{\omega}=\mathrm{2}{isin}\left(\theta\right) \\ $$$$\:\:\:{corallary}\::\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({Im}\left(\frac{\omega^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{w}}\right)\right){d}\theta=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\checkmark \\ $$
Answered by Ar Brandon last updated on 04/Dec/20
![f(ω)=(1+ω)^n =(1+cosθ+isinθ)^n =(2cos^2 (θ/2)+2isin(θ/2)cos(θ/2))^n =[2cos(θ/2)(cos(θ/2)+isin(θ/2))]^n =2^n cos^n (θ/2)e^(i((nθ)/2))](https://www.tinkutara.com/question/Q124599.png)
$$\mathrm{f}\left(\omega\right)=\left(\mathrm{1}+\omega\right)^{\mathrm{n}} =\left(\mathrm{1}+\mathrm{cos}\theta+\mathrm{isin}\theta\right)^{\mathrm{n}} \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{2cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\mathrm{2isin}\frac{\theta}{\mathrm{2}}\mathrm{cos}\frac{\theta}{\mathrm{2}}\right)^{\mathrm{n}} \\ $$$$\:\:\:\:\:\:\:\:\:=\left[\mathrm{2cos}\frac{\theta}{\mathrm{2}}\left(\mathrm{cos}\frac{\theta}{\mathrm{2}}+\mathrm{isin}\frac{\theta}{\mathrm{2}}\right)\right]^{\mathrm{n}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{n}} \mathrm{cos}^{\mathrm{n}} \frac{\theta}{\mathrm{2}}\mathrm{e}^{\mathrm{i}\frac{\mathrm{n}\theta}{\mathrm{2}}} \\ $$
Commented by Ar Brandon last updated on 04/Dec/20
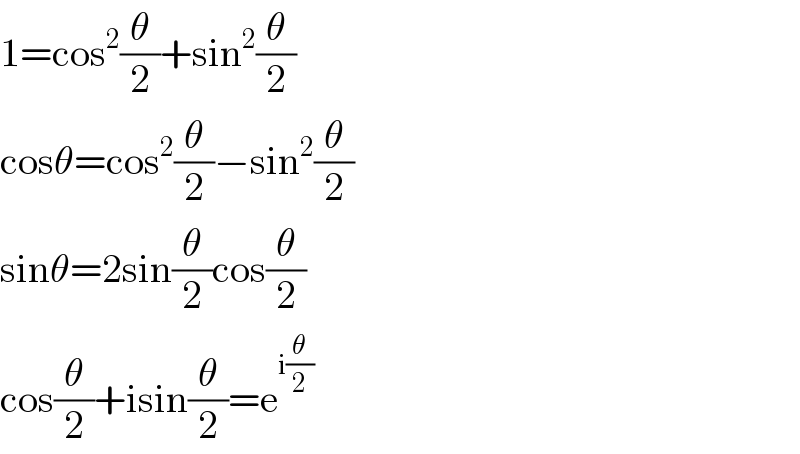
$$\mathrm{1}=\mathrm{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\mathrm{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{cos}\theta=\mathrm{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{sin}\theta=\mathrm{2sin}\frac{\theta}{\mathrm{2}}\mathrm{cos}\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{cos}\frac{\theta}{\mathrm{2}}+\mathrm{isin}\frac{\theta}{\mathrm{2}}=\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} \\ $$
Answered by mnjuly1970 last updated on 04/Dec/20
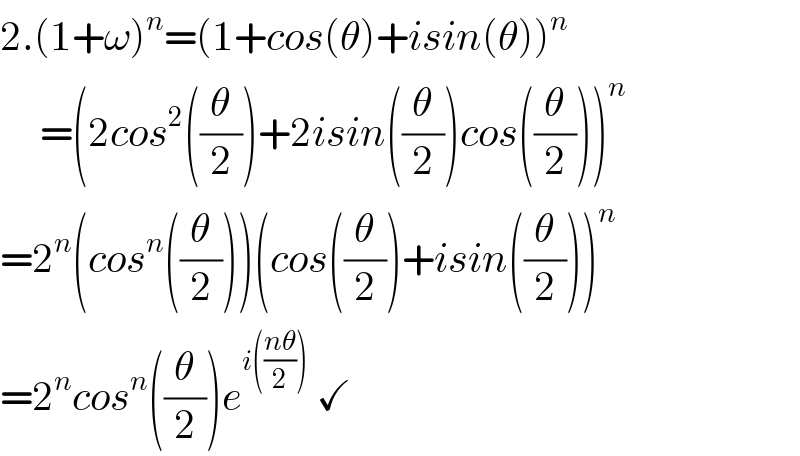
$$\mathrm{2}.\left(\mathrm{1}+\omega\right)^{{n}} =\left(\mathrm{1}+{cos}\left(\theta\right)+{isin}\left(\theta\right)\right)^{{n}} \\ $$$$\:\:\:\:\:=\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{2}{isin}\left(\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{{n}} \\ $$$$=\mathrm{2}^{{n}} \left({cos}^{{n}} \left(\frac{\theta}{\mathrm{2}}\right)\right)\left({cos}\left(\frac{\theta}{\mathrm{2}}\right)+{isin}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{{n}} \\ $$$$=\mathrm{2}^{{n}} {cos}^{{n}} \left(\frac{\theta}{\mathrm{2}}\right){e}^{{i}\left(\frac{{n}\theta}{\mathrm{2}}\right)} \:\checkmark \\ $$
