Question Number 155809 by zainaltanjung last updated on 05/Oct/21
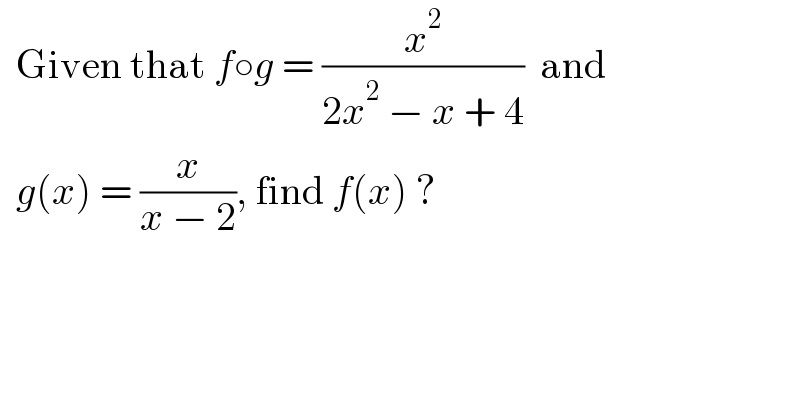
$$\:\:\mathrm{Given}\:\mathrm{that}\:{f}\circ{g}\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{4}}\:\:\mathrm{and} \\ $$$$\:\:{g}\left({x}\right)\:=\:\frac{{x}}{{x}\:−\:\mathrm{2}},\:\mathrm{find}\:{f}\left({x}\right)\:? \\ $$$$ \\ $$
Answered by PRITHWISH SEN 2 last updated on 05/Oct/21
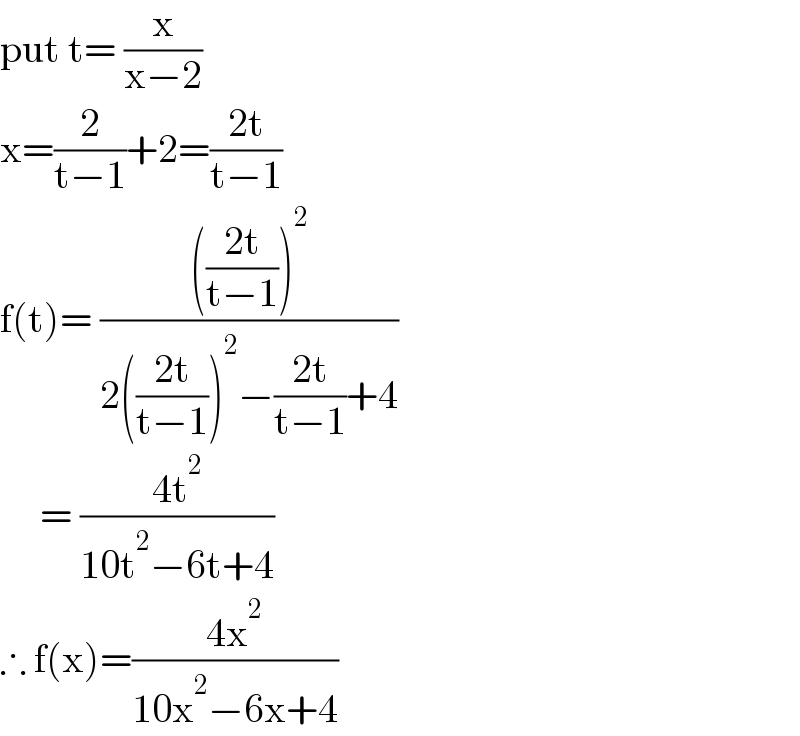
$$\mathrm{put}\:\mathrm{t}=\:\frac{\mathrm{x}}{\mathrm{x}−\mathrm{2}} \\ $$$$\mathrm{x}=\frac{\mathrm{2}}{\mathrm{t}−\mathrm{1}}+\mathrm{2}=\frac{\mathrm{2t}}{\mathrm{t}−\mathrm{1}}\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\:\frac{\left(\frac{\mathrm{2t}}{\mathrm{t}−\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{2}\left(\frac{\mathrm{2t}}{\mathrm{t}−\mathrm{1}}\right)^{\mathrm{2}} −\frac{\mathrm{2t}}{\mathrm{t}−\mathrm{1}}+\mathrm{4}} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{4t}^{\mathrm{2}} }{\mathrm{10t}^{\mathrm{2}} −\mathrm{6t}+\mathrm{4}} \\ $$$$\therefore\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{4x}^{\mathrm{2}} }{\mathrm{10x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{4}} \\ $$
