Question Number 119391 by Don08q last updated on 24/Oct/20

$$\:\mathrm{Given}\:\mathrm{that}\:{f}\left({x}−\mathrm{3}\right)\:=\:{x}^{\mathrm{2}} \:−\:\mathrm{12}{x}\:+\:\mathrm{41} \\ $$$$\:\mathrm{find}\:\mathrm{an}\:\mathrm{explicit}\:\mathrm{expression}\:\mathrm{for}\:{f}\left({x}\right) \\ $$$$ \\ $$$$\:{please}\:{I}\:\:{need}\:{the}\:{procedure} \\ $$
Answered by bemath last updated on 24/Oct/20
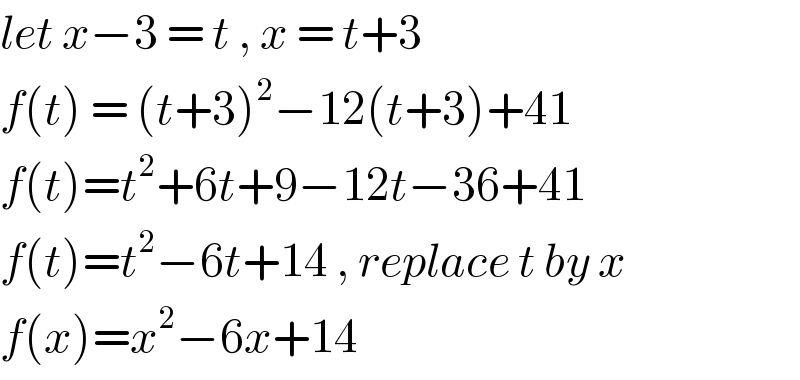
$${let}\:{x}−\mathrm{3}\:=\:{t}\:,\:{x}\:=\:{t}+\mathrm{3}\: \\ $$$${f}\left({t}\right)\:=\:\left({t}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{12}\left({t}+\mathrm{3}\right)+\mathrm{41} \\ $$$${f}\left({t}\right)={t}^{\mathrm{2}} +\mathrm{6}{t}+\mathrm{9}−\mathrm{12}{t}−\mathrm{36}+\mathrm{41} \\ $$$${f}\left({t}\right)={t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{14}\:,\:{replace}\:{t}\:{by}\:{x}\: \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{14} \\ $$
Commented by Don08q last updated on 24/Oct/20
$${Thanks}\:{very}\:{much}\:{Sir} \\ $$
