Question Number 39700 by Rio Mike last updated on 10/Jul/18
![given that f(x)= x^3 − 3x^2 + ax + b and (x−1) is a factor of f(x) also the maximum value of f(x) at poin where x = 1 is 12 find a) (dy/d) (f(x)) b) the values of a and b c) factorise f(x) completely d) hence evaluate ∫_3 ^4 [f(x)] dx](https://www.tinkutara.com/question/Q39700.png)
$${given}\:{that}\:{f}\left({x}\right)=\:{x}^{\mathrm{3}} \:−\:\mathrm{3}{x}^{\mathrm{2}} \:+\:{ax}\:+\:{b} \\ $$$${and}\:\left({x}−\mathrm{1}\right)\:{is}\:{a}\:{factor}\:{of}\:{f}\left({x}\right) \\ $$$${also}\:{the}\:{maximum}\:{value}\:{of} \\ $$$${f}\left({x}\right)\:{at}\:{poin}\:{where}\:{x}\:=\:\mathrm{1} \\ $$$${is}\:\mathrm{12}\:{find}\: \\ $$$$\left.{a}\right)\:\frac{{dy}}{{d}}\:\left({f}\left({x}\right)\right) \\ $$$$\left.{b}\right)\:{the}\:{values}\:{of}\:{a}\:{and}\:{b} \\ $$$$\left.{c}\right)\:{factorise}\:{f}\left({x}\right)\:{completely} \\ $$$$\left.{d}\right)\:{hence}\:{evaluate}\:\int_{\mathrm{3}} ^{\mathrm{4}} \left[{f}\left({x}\right)\right]\:{dx} \\ $$
Commented by jorge160895@hotmail.com last updated on 10/Jul/18
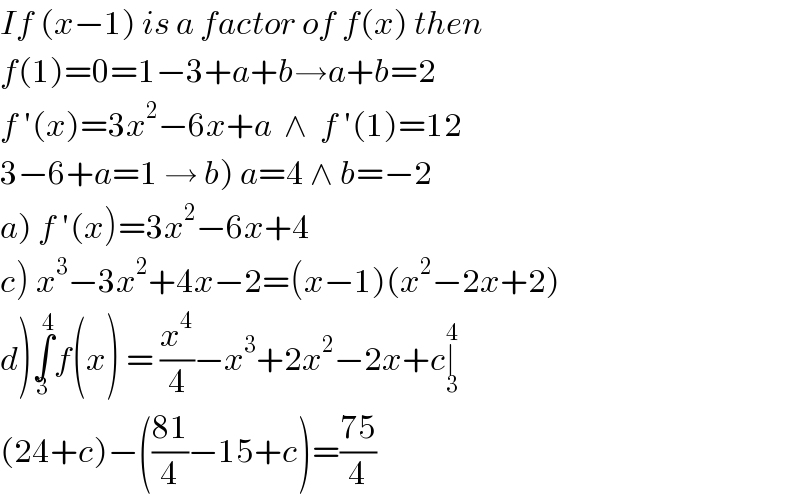
$${If}\:\left({x}−\mathrm{1}\right)\:{is}\:{a}\:{factor}\:{of}\:{f}\left({x}\right)\:{then} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0}=\mathrm{1}−\mathrm{3}+{a}+{b}\rightarrow{a}+{b}=\mathrm{2} \\ $$$${f}\:'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}+{a}\:\:\wedge\:\:{f}\:'\left(\mathrm{1}\right)=\mathrm{12} \\ $$$$\left.\mathrm{3}−\mathrm{6}+{a}=\mathrm{1}\:\rightarrow\:{b}\right)\:{a}=\mathrm{4}\:\wedge\:{b}=−\mathrm{2} \\ $$$$\left.{a}\right)\:{f}\:'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{4}\: \\ $$$$\left.{c}\right)\:{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{2}=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\right) \\ $$$$\left.{d}\right)\underset{\mathrm{3}} {\overset{\mathrm{4}} {\int}}{f}\left({x}\right)\:=\:\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+{c}\underset{\mathrm{3}} {\overset{\mathrm{4}} {\mid}} \\ $$$$\left(\mathrm{24}+{c}\right)−\left(\frac{\mathrm{81}}{\mathrm{4}}−\mathrm{15}+{c}\right)=\frac{\mathrm{75}}{\mathrm{4}} \\ $$
