Given-that-LCM-A-B-C-252-LCM-A-B-36-amp-LCM-A-C-63-then-LCM-B-C-Pl-determine-all-possible-answers-

Question Number 30687 by Rasheed.Sindhi last updated on 24/Feb/18

Given that LCM (A, B, C) = 252

LCM (A, B) = 36 & LCM (A, C) = 63;

then :

LCM (B, C) = ?

Pl determine all possible answers .

Answered by MJS last updated on 24/Feb/18

252 = 2^{2} 3^{2} 7

36 = 2^{2} 3^{2}

63 = 3^{2} 7

{A, B} = {4, 9} \lor {9, 4} \lor {1, 36} \lor {36, 1}

{A, C} = {7, 9} \lor {9, 7} \lor {1, 63} \lor {63, 1}

A = 9

B = 4

C = 7

L C M (4, 7) = 28

or

A = 1

B = 36

C = 63

L C M (36, 63) = 252

Commented by Rasheed.Sindhi last updated on 24/Feb/18

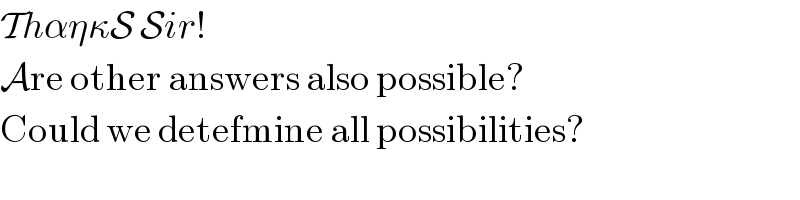
T h α η κ S S i r!

A re other answers also possible ?

Could we detefmine all possibilities ?

Commented by MJS last updated on 24/Feb/18

sorry, even more possibilities :

if A or B = 36 the other one can be

1, 2, 3, 4, 6, 9, 12, 18 or 36

if A or C = 63 the other one can be

1, 3, 7, 9, 21 or 63

so also possible :

{A, B, C} = {3, 36, 63} \lor {9, 36, 63}

but the L C M (B, C) is 252 too

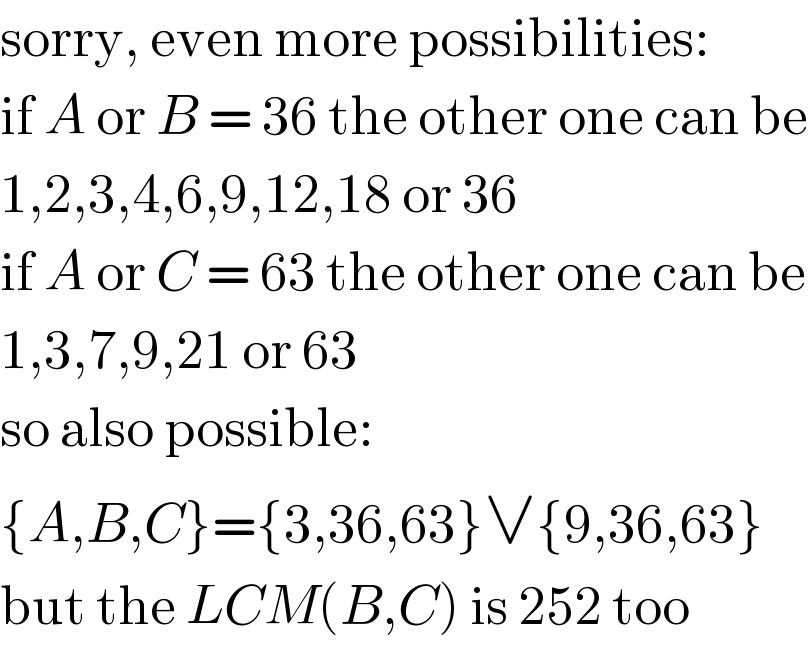
Commented by soksan last updated on 25/Feb/18

252 = 2^{2} 3^{2} 7

Facebook Tweet Pin