Question Number 80172 by Rio Michael last updated on 31/Jan/20
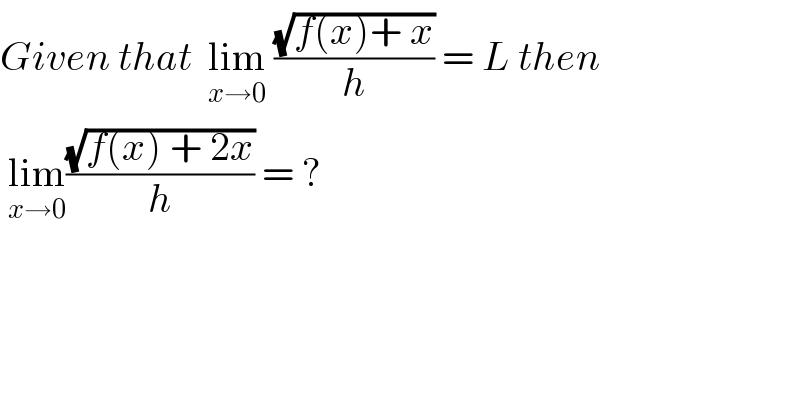
$${Given}\:{that}\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{f}\left({x}\right)+\:{x}}}{{h}}\:=\:{L}\:{then} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{{f}\left({x}\right)\:+\:\mathrm{2}{x}}}{{h}}\:=\:? \\ $$
Commented by john santu last updated on 31/Jan/20
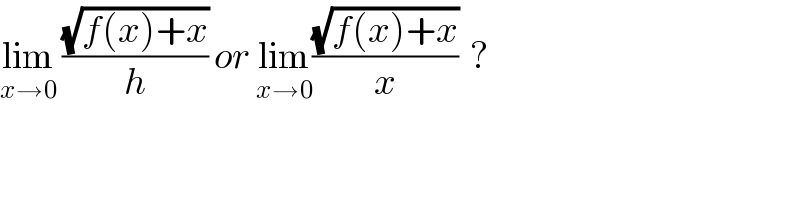
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{f}\left({x}\right)+{x}}}{{h}}\:{or}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{{f}\left({x}\right)+{x}}}{{x}}\:\:? \\ $$
Commented by john santu last updated on 31/Jan/20
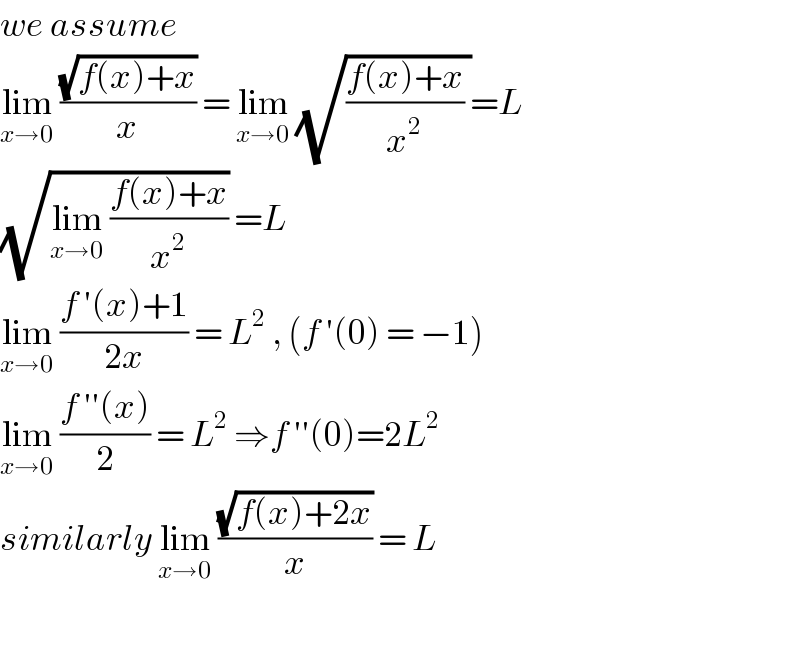
$${we}\:{assume}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{f}\left({x}\right)+{x}}}{{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{{f}\left({x}\right)+{x}}{{x}^{\mathrm{2}} }\:}={L} \\ $$$$\sqrt{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)+{x}}{{x}^{\mathrm{2}} }}\:={L} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\:'\left({x}\right)+\mathrm{1}}{\mathrm{2}{x}}\:=\:{L}^{\mathrm{2}} \:,\:\left({f}\:'\left(\mathrm{0}\right)\:=\:−\mathrm{1}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\:''\left({x}\right)}{\mathrm{2}}\:=\:{L}^{\mathrm{2}} \:\Rightarrow{f}\:''\left(\mathrm{0}\right)=\mathrm{2}{L}^{\mathrm{2}} \\ $$$${similarly}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{f}\left({x}\right)+\mathrm{2}{x}}}{{x}}\:=\:{L} \\ $$$$ \\ $$
