Given-that-the-curve-y-2x-2-19x-18-does-not-intersect-the-line-y-x-k-find-the-largest-integer-of-k-

Question Number 120705 by ZiYangLee last updated on 02/Nov/20

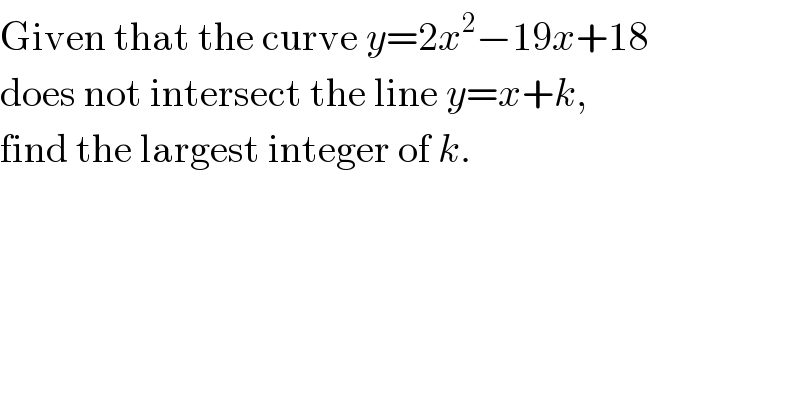
$$\mathrm{Given}\:\mathrm{that}\:\mathrm{the}\:\mathrm{curve}\:{y}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{19}{x}+\mathrm{18} \\ $$$$\mathrm{does}\:\mathrm{not}\:\mathrm{intersect}\:\mathrm{the}\:\mathrm{line}\:{y}={x}+{k}, \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{integer}\:\mathrm{of}\:{k}. \\ $$

Commented by john santu last updated on 02/Nov/20

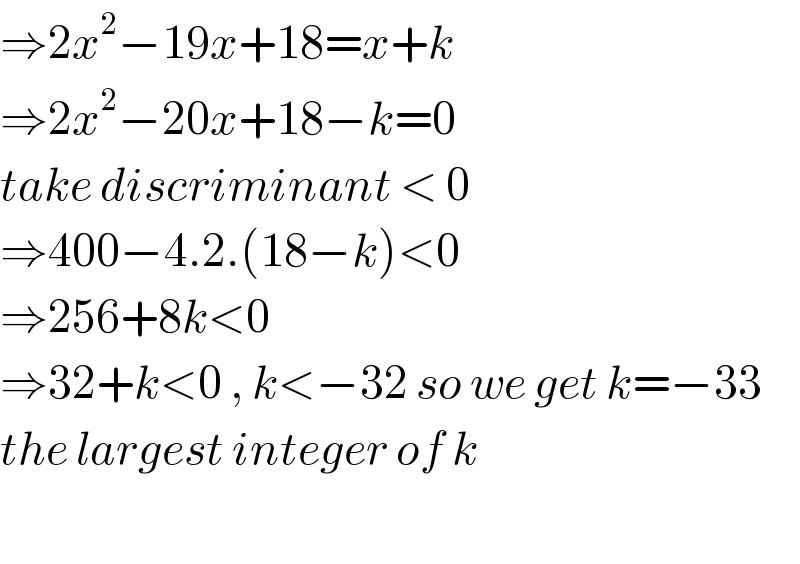
⇒2x^2 −19x+18=x+k ⇒2x^2 −20x+18−k=0 take discriminant < 0 ⇒400−4.2.(18−k)<0 ⇒256+8k<0 ⇒32+k<0 , k<−32 so we get k=−33 the largest integer of k

$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −\mathrm{19}{x}+\mathrm{18}={x}+{k} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −\mathrm{20}{x}+\mathrm{18}−{k}=\mathrm{0} \\ $$$${take}\:{discriminant}\:<\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{400}−\mathrm{4}.\mathrm{2}.\left(\mathrm{18}−{k}\right)<\mathrm{0} \\ $$$$\Rightarrow\mathrm{256}+\mathrm{8}{k}<\mathrm{0} \\ $$$$\Rightarrow\mathrm{32}+{k}<\mathrm{0}\:,\:{k}<−\mathrm{32}\:{so}\:{we}\:{get}\:{k}=−\mathrm{33} \\ $$$${the}\:{largest}\:{integer}\:{of}\:{k} \\ $$$$ \\ $$

Facebook Tweet Pin

Given-that-the-curve-y-2x-2-19x-18-does-not-intersect-the-line-y-x-k-find-the-largest-integer-of-k-

Leave a Reply Cancel reply