Question Number 169303 by Mastermind last updated on 28/Apr/22
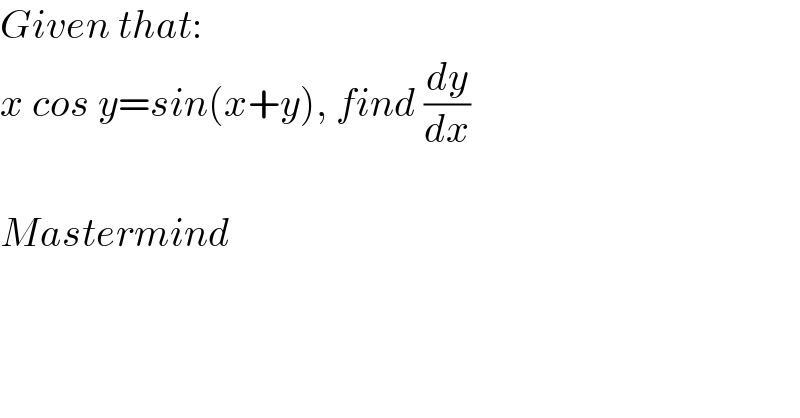
$${Given}\:{that}: \\ $$$${x}\:{cos}\:{y}={sin}\left({x}+{y}\right),\:{find}\:\frac{{dy}}{{dx}} \\ $$$$ \\ $$$${Mastermind} \\ $$
Commented by infinityaction last updated on 28/Apr/22

$${x}\:=\:\frac{\mathrm{sin}\:{x}\mathrm{cos}\:{y}+\mathrm{sin}\:{y}\mathrm{cos}\:{x}}{\mathrm{cos}\:{y}} \\ $$$${x}\:=\:\mathrm{sin}\:{x}\:+\:\mathrm{tan}\:{y}\mathrm{cos}\:{x} \\ $$$${x}\mathrm{sec}\:{x}\:−\mathrm{tan}\:{x}\:=\:\mathrm{tan}\:{y} \\ $$$${D}.{W}.{R}.{T}.{X} \\ $$$$\mathrm{sec}\:^{\mathrm{2}} {y}\:\frac{{dy}}{{dx}}\:=\:{x}\:\mathrm{sec}\:{x}\mathrm{tan}\:{x}\:+\:\mathrm{sec}\:{x}−\:\mathrm{sec}\:^{\mathrm{2}} {x} \\ $$$$\frac{{dy}}{{dx}\:}\:=\:\mathrm{sec}\:{x}\left(\frac{{x}\mathrm{tan}\:{x}−\mathrm{sec}\:{x}+\mathrm{1}}{\mathrm{sec}\:^{\mathrm{2}} {y}}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 28/Apr/22
![cos y−x sin y (dy/dx)=cos (x+y)(1+ (dy/dx)) cos y−cos (x+y)=[x sin y+cos (x+y)] (dy/dx) (dy/dx)=((cos y−cos (x+y))/(x sin y+cos (x+y)))](https://www.tinkutara.com/question/Q169331.png)
$$\mathrm{cos}\:{y}−{x}\:\mathrm{sin}\:{y}\:\frac{{dy}}{{dx}}=\mathrm{cos}\:\left({x}+{y}\right)\left(\mathrm{1}+\:\frac{{dy}}{{dx}}\right) \\ $$$$\mathrm{cos}\:{y}−\mathrm{cos}\:\left({x}+{y}\right)=\left[{x}\:\mathrm{sin}\:{y}+\mathrm{cos}\:\left({x}+{y}\right)\right]\:\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{cos}\:{y}−\mathrm{cos}\:\left({x}+{y}\right)}{{x}\:\mathrm{sin}\:{y}+\mathrm{cos}\:\left({x}+{y}\right)} \\ $$
