Given-that-x-tan-23-find-the-value-of-cos-16-in-terms-of-x-

Question Number 144614 by nadovic last updated on 27/Jun/21

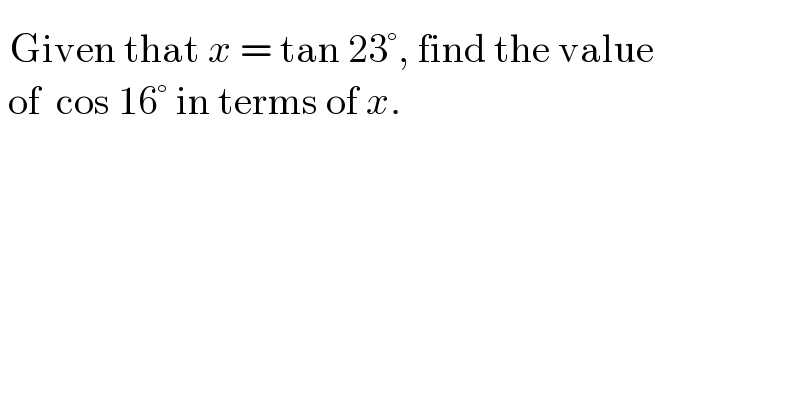
\overset{}{} Given that x = \tan 23 °, find the value

of \cos 16 ° in terms of x \underset{}{.}

Answered by qaz last updated on 27/Jun/21

x = \tan 23 ° = \frac{\tan 30 ° - \tan 7 °}{1 + \tan 30 ° \cdot \tan 7 °}

\Rightarrow \tan 7 ° = \frac{\tan 30 ° - x}{1 + xtan 30 °}

\tan 16 ° = \frac{\tan 23 ° - \tan 7 °}{1 + \tan 23 ° \cdot \tan 7 °} = \frac{x - \tan 7 °}{1 + xtan 7 °}

\Rightarrow \cos 16 ° = \frac{1}{\sqrt{1 + \tan^{2} 16 °}}

= \frac{1}{\sqrt{1 + {(\frac{x - \tan 7 °}{1 + xtan 7 °})}^{2}}}

= \frac{1}{\sqrt{1 + {(\frac{x - \frac{\tan 30 ° - x}{1 + xtan 30 °}}{1 + x \cdot \frac{\tan 30 ° - x}{1 + xtan 30 °}})}^{2}}}

continue \dots

Commented by nadovic last updated on 27/Jun/21

T h a n k y o u S i r

Answered by imjagoll last updated on 27/Jun/21

\cos 16 ° = \cos (23 ° - 7 °)

= \cos 23 ° \cos 7 ° + \sin 23 ° \sin 7 °

\tan 7 ° = \frac{\frac{1}{\sqrt{3}} - x}{1 + \frac{1}{\sqrt{3}} x} = \frac{1 - x \sqrt{3}}{\sqrt{3} + x}

{\begin{cases} \sin 23 ° = \frac{x}{\sqrt{1 + x^{2}}} \\ \cos 23 ° = \frac{1}{\sqrt{1 + x^{2}}} \end{cases}

{\begin{cases} \sin 7 ° = \frac{1 - x \sqrt{3}}{2 \sqrt{x^{2} + 1}} \\ \cos 7 ° = \frac{x + \sqrt{3}}{2 \sqrt{x^{2} + 1}} \end{cases}

\cos 16 ° = \frac{1}{\sqrt{1 + x^{2}}} . \frac{x + \sqrt{3}}{2 \sqrt{1 + x^{2}}} + \frac{x}{\sqrt{1 + x^{2}}} . \frac{1 - x \sqrt{3}}{2 \sqrt{1 + x^{2}}}

= \frac{x + \sqrt{3} + x - x^{2} \sqrt{3}}{2 (1 + x^{2})} = \frac{2 x + \sqrt{3} - x^{2} \sqrt{3}}{2 + {2 x}^{2}}

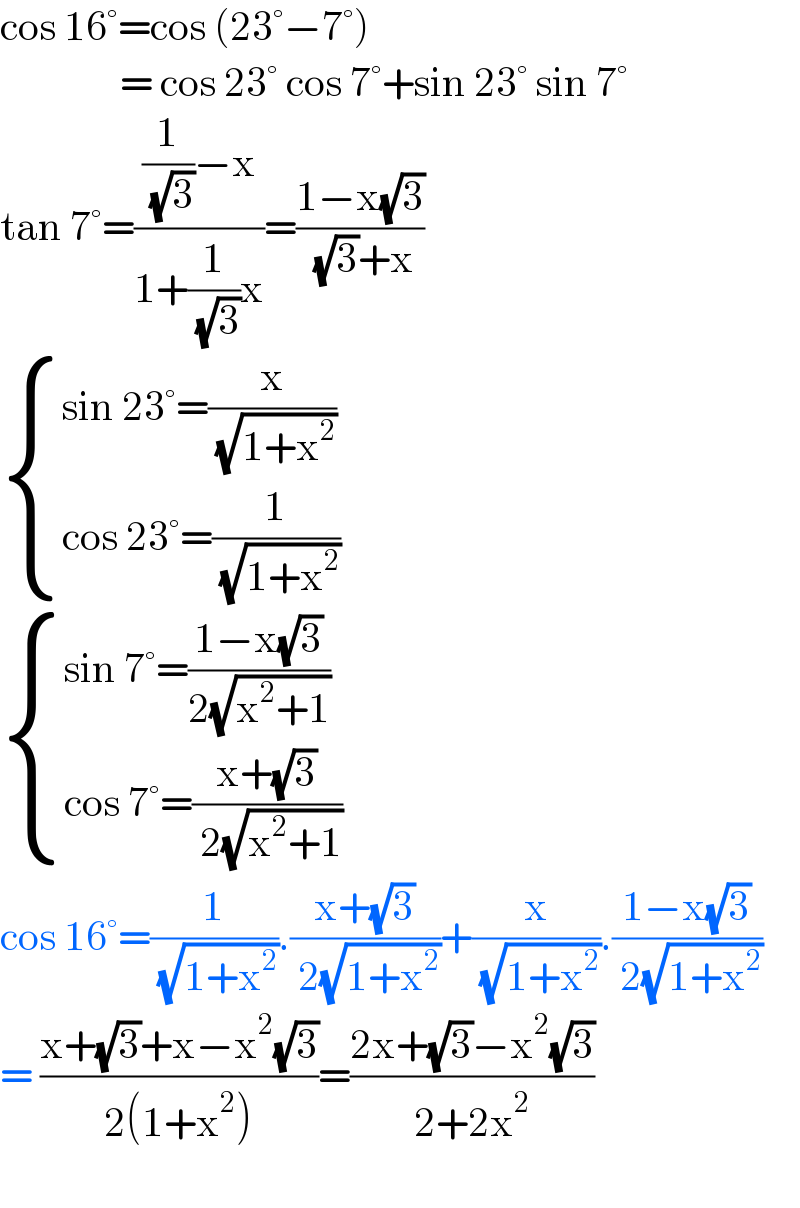
Commented by liberty last updated on 27/Jun/21

for x = \tan 23 ° \approx . 424

\cos 16 ° = \frac{2 (. 424) + \sqrt{3} - \sqrt{3} {(. 424)}^{2}}{2 (1 + {(. 424)}^{2})}

\approx . 9615

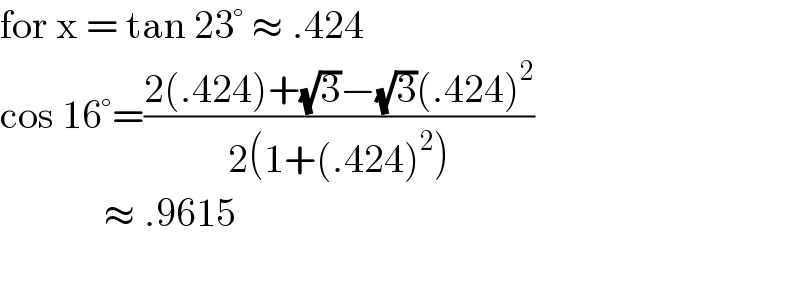
Commented by nadovic last updated on 27/Jun/21

T h a n k y o u S i r

Facebook Tweet Pin