Question Number 160659 by ZiYangLee last updated on 04/Dec/21
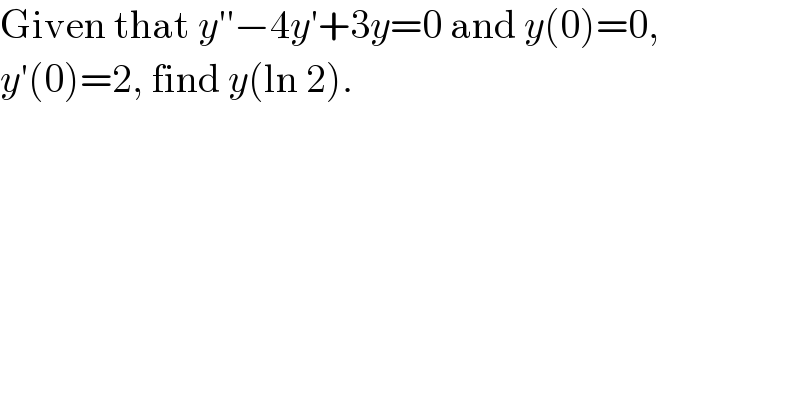
$$\mathrm{Given}\:\mathrm{that}\:{y}''−\mathrm{4}{y}'+\mathrm{3}{y}=\mathrm{0}\:\mathrm{and}\:{y}\left(\mathrm{0}\right)=\mathrm{0}, \\ $$$${y}'\left(\mathrm{0}\right)=\mathrm{2},\:\mathrm{find}\:{y}\left(\mathrm{ln}\:\mathrm{2}\right). \\ $$
Answered by mr W last updated on 04/Dec/21
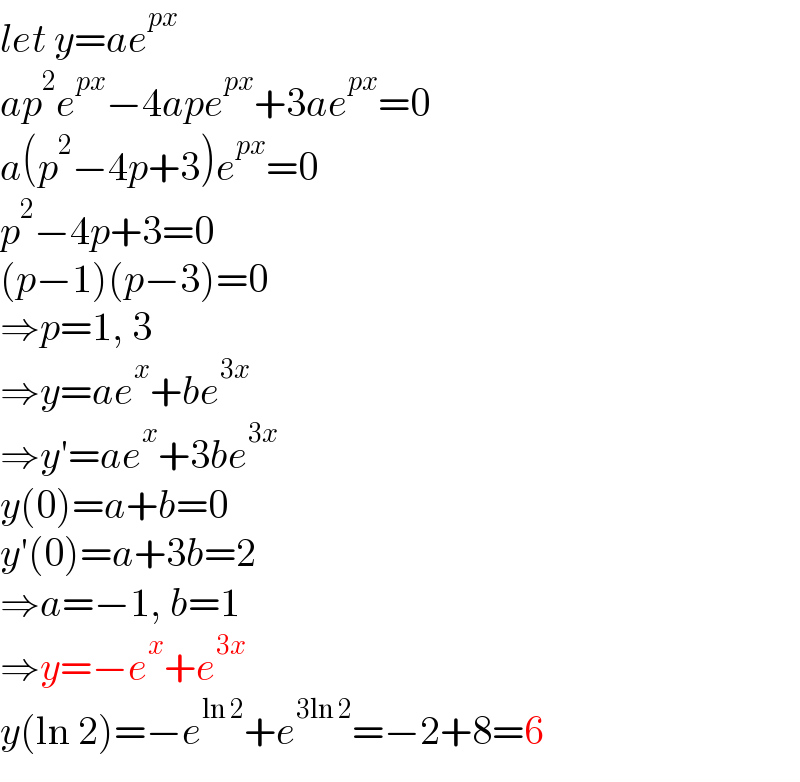
$${let}\:{y}={ae}^{{px}} \\ $$$${ap}^{\mathrm{2}} {e}^{{px}} −\mathrm{4}{ape}^{{px}} +\mathrm{3}{ae}^{{px}} =\mathrm{0} \\ $$$${a}\left({p}^{\mathrm{2}} −\mathrm{4}{p}+\mathrm{3}\right){e}^{{px}} =\mathrm{0} \\ $$$${p}^{\mathrm{2}} −\mathrm{4}{p}+\mathrm{3}=\mathrm{0} \\ $$$$\left({p}−\mathrm{1}\right)\left({p}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}=\mathrm{1},\:\mathrm{3} \\ $$$$\Rightarrow{y}={ae}^{{x}} +{be}^{\mathrm{3}{x}} \\ $$$$\Rightarrow{y}'={ae}^{{x}} +\mathrm{3}{be}^{\mathrm{3}{x}} \\ $$$${y}\left(\mathrm{0}\right)={a}+{b}=\mathrm{0} \\ $$$${y}'\left(\mathrm{0}\right)={a}+\mathrm{3}{b}=\mathrm{2} \\ $$$$\Rightarrow{a}=−\mathrm{1},\:{b}=\mathrm{1} \\ $$$$\Rightarrow{y}=−{e}^{{x}} +{e}^{\mathrm{3}{x}} \\ $$$${y}\left(\mathrm{ln}\:\mathrm{2}\right)=−{e}^{\mathrm{ln}\:\mathrm{2}} +{e}^{\mathrm{3ln}\:\mathrm{2}} =−\mathrm{2}+\mathrm{8}=\mathrm{6} \\ $$
