Question Number 146771 by ZiYangLee last updated on 15/Jul/21
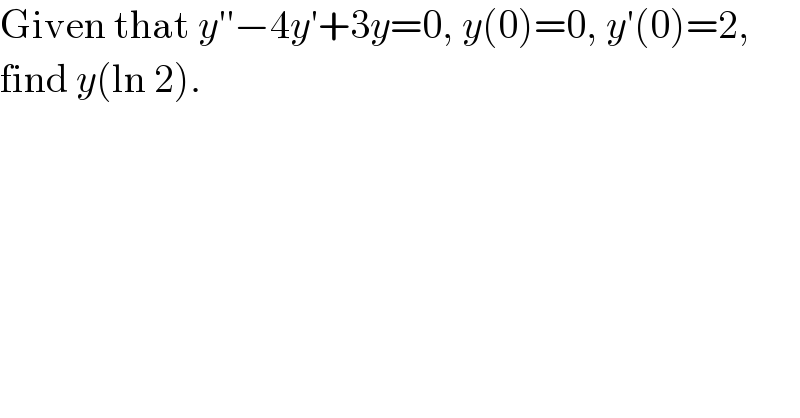
$$\mathrm{Given}\:\mathrm{that}\:{y}''−\mathrm{4}{y}'+\mathrm{3}{y}=\mathrm{0},\:{y}\left(\mathrm{0}\right)=\mathrm{0},\:{y}'\left(\mathrm{0}\right)=\mathrm{2}, \\ $$$$\mathrm{find}\:{y}\left(\mathrm{ln}\:\mathrm{2}\right). \\ $$
Answered by mathmax by abdo last updated on 15/Jul/21
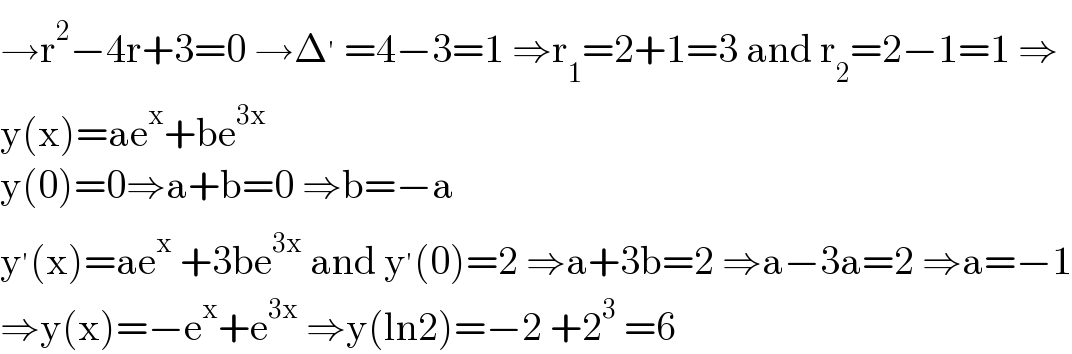
$$\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{4r}+\mathrm{3}=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{4}−\mathrm{3}=\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\mathrm{2}+\mathrm{1}=\mathrm{3}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{2}−\mathrm{1}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{ae}^{\mathrm{x}} +\mathrm{be}^{\mathrm{3x}} \\ $$$$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{0}\:\Rightarrow\mathrm{b}=−\mathrm{a} \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)=\mathrm{ae}^{\mathrm{x}} \:+\mathrm{3be}^{\mathrm{3x}} \:\mathrm{and}\:\mathrm{y}^{'} \left(\mathrm{0}\right)=\mathrm{2}\:\Rightarrow\mathrm{a}+\mathrm{3b}=\mathrm{2}\:\Rightarrow\mathrm{a}−\mathrm{3a}=\mathrm{2}\:\Rightarrow\mathrm{a}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=−\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{\mathrm{3x}} \:\Rightarrow\mathrm{y}\left(\mathrm{ln2}\right)=−\mathrm{2}\:+\mathrm{2}^{\mathrm{3}} \:=\mathrm{6} \\ $$
