Question Number 20832 by j.masanja06@gmail.com last updated on 04/Sep/17
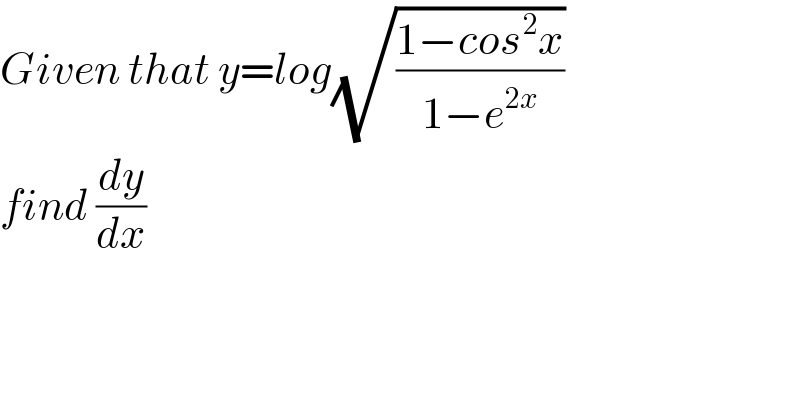
$${Given}\:{that}\:{y}={log}\sqrt{\frac{\mathrm{1}−{cos}^{\mathrm{2}} {x}}{\mathrm{1}−{e}^{\mathrm{2}{x}} }} \\ $$$${find}\:\frac{{dy}}{{dx}} \\ $$
Commented by myintkhaing last updated on 04/Sep/17

$$\mathrm{ecos}^{\mathrm{2}} \mathrm{x}\:??? \\ $$
Commented by geovane10math last updated on 05/Sep/17
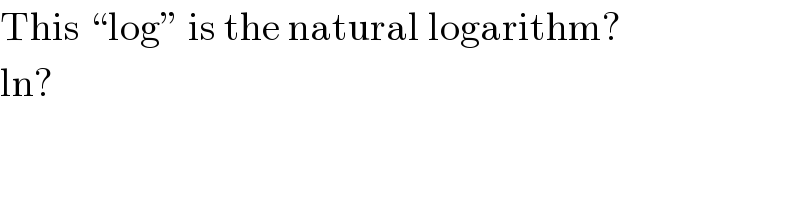
$$\mathrm{This}\:“\mathrm{log}''\:\mathrm{is}\:\mathrm{the}\:\mathrm{natural}\:\mathrm{logarithm}? \\ $$$$\mathrm{ln}? \\ $$
Answered by Hitler last updated on 05/Sep/17
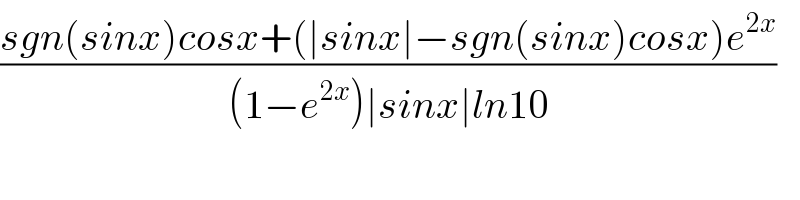
$$\frac{{sgn}\left({sinx}\right){cosx}+\left(\mid{sinx}\mid−{sgn}\left({sinx}\right){cosx}\right){e}^{\mathrm{2}{x}} }{\left(\mathrm{1}−{e}^{\mathrm{2}{x}} \right)\mid{sinx}\mid{ln}\mathrm{10}} \\ $$
Answered by myintkhaing last updated on 05/Sep/17
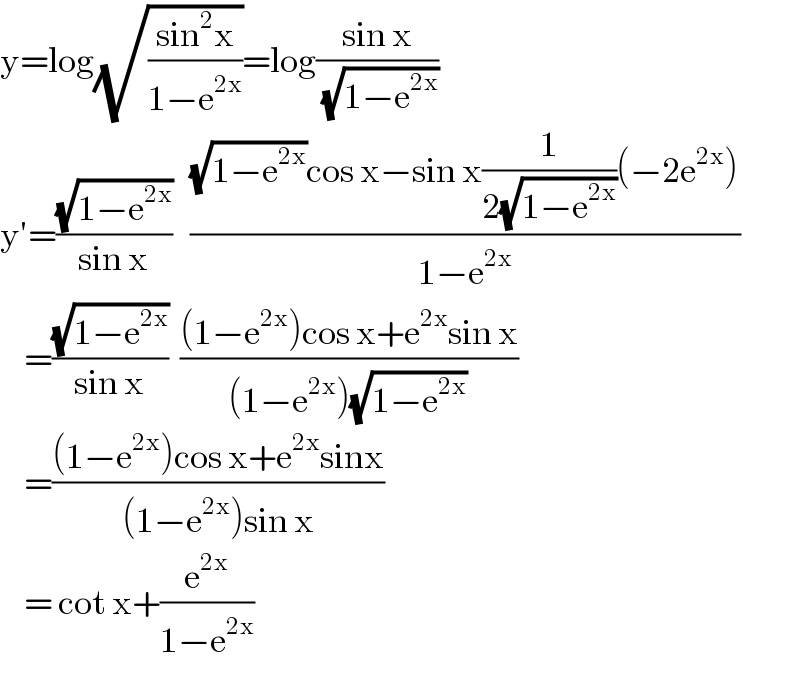
$$\mathrm{y}=\mathrm{log}\sqrt{\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} }}=\mathrm{log}\frac{\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} }} \\ $$$$\mathrm{y}'=\frac{\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} }}{\mathrm{sin}\:\mathrm{x}}\:\:\:\frac{\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} }\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} }}\left(−\mathrm{2e}^{\mathrm{2x}} \right)}{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} } \\ $$$$\:\:\:\:=\frac{\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} }}{\mathrm{sin}\:\mathrm{x}}\:\:\frac{\left(\mathrm{1}−\mathrm{e}^{\mathrm{2x}} \right)\mathrm{cos}\:\mathrm{x}+\mathrm{e}^{\mathrm{2x}} \mathrm{sin}\:\mathrm{x}}{\left(\mathrm{1}−\mathrm{e}^{\mathrm{2x}} \right)\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} }} \\ $$$$\:\:\:\:=\frac{\left(\mathrm{1}−\mathrm{e}^{\mathrm{2x}} \right)\mathrm{cos}\:\mathrm{x}+\mathrm{e}^{\mathrm{2x}} \mathrm{sinx}}{\left(\mathrm{1}−\mathrm{e}^{\mathrm{2x}} \right)\mathrm{sin}\:\mathrm{x}} \\ $$$$\:\:\:\:=\:\mathrm{cot}\:\mathrm{x}+\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{1}−\mathrm{e}^{\mathrm{2x}} } \\ $$
