Question Number 33005 by Rio Mike last updated on 09/Apr/18
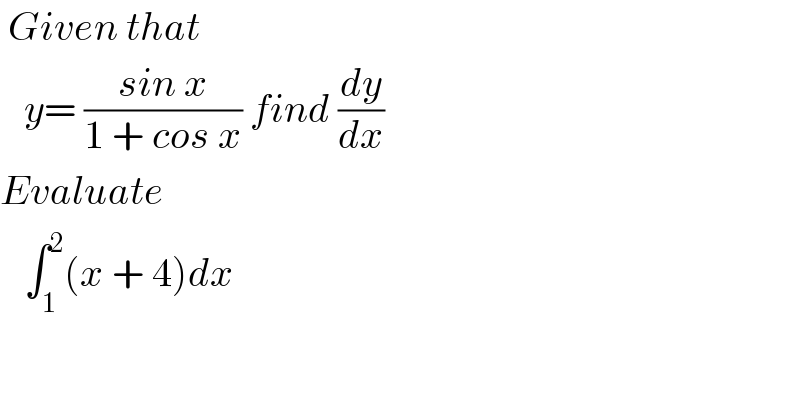
$$\:{Given}\:{that}\: \\ $$$$\:\:\:{y}=\:\frac{{sin}\:{x}}{\mathrm{1}\:+\:{cos}\:{x}}\:{find}\:\frac{{dy}}{{dx}} \\ $$$${Evaluate}\: \\ $$$$\:\:\:\int_{\mathrm{1}} ^{\mathrm{2}} \left({x}\:+\:\mathrm{4}\right){dx} \\ $$
Commented by abdo imad last updated on 09/Apr/18
![(dy/dx) = ((cosx(1+cosx) +sin^2 x)/((1+cosx)^2 )) = ((cosx +sin^2 x +cos^2 x)/((1+cosx)^2 )) . = ((1+cosx)/((1+cosx)^2 )) = (1/(1+cosx)) for x∈ D_y . ★ ∫_1 ^2 (x+4)dx =[ (x^2 /2) +4x]_1 ^2 =2 +8 −(1/2) −4 = (3/2) +4 = ((11)/2) .](https://www.tinkutara.com/question/Q33010.png)
$$\frac{{dy}}{{dx}}\:=\:\frac{{cosx}\left(\mathrm{1}+{cosx}\right)\:+{sin}^{\mathrm{2}} {x}}{\left(\mathrm{1}+{cosx}\right)^{\mathrm{2}} }\:=\:\frac{{cosx}\:+{sin}^{\mathrm{2}} {x}\:\:+{cos}^{\mathrm{2}} {x}}{\left(\mathrm{1}+{cosx}\right)^{\mathrm{2}} }\:\:. \\ $$$$=\:\frac{\mathrm{1}+{cosx}}{\left(\mathrm{1}+{cosx}\right)^{\mathrm{2}} }\:=\:\:\frac{\mathrm{1}}{\mathrm{1}+{cosx}}\:{for}\:{x}\in\:{D}_{{y}} \:\:. \\ $$$$\bigstar\:\:\int_{\mathrm{1}} ^{\mathrm{2}} \left({x}+\mathrm{4}\right){dx}\:=\left[\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{4}{x}\right]_{\mathrm{1}} ^{\mathrm{2}} \:=\mathrm{2}\:+\mathrm{8}\:−\frac{\mathrm{1}}{\mathrm{2}}\:−\mathrm{4} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}}\:+\mathrm{4}\:=\:\frac{\mathrm{11}}{\mathrm{2}}\:\:. \\ $$
