Question Number 116685 by mathocean1 last updated on 05/Oct/20
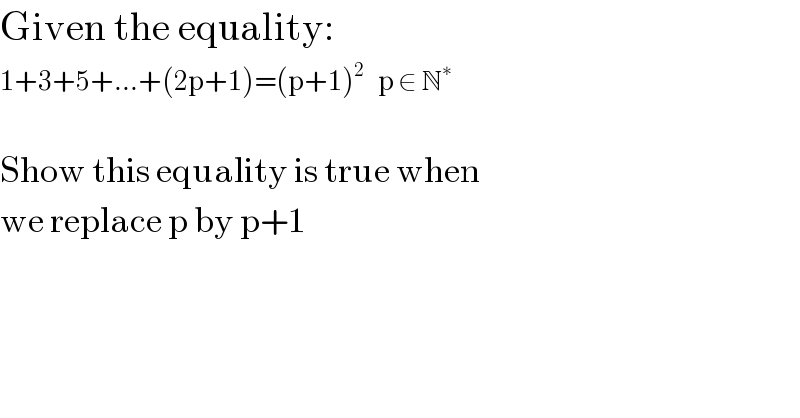
$$\mathrm{Given}\:\mathrm{the}\:\mathrm{equality}: \\ $$$$\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\left(\mathrm{2p}+\mathrm{1}\right)=\left(\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}\:} \:\:\:\mathrm{p}\:\in\:\mathbb{N}^{\ast} \\ $$$$ \\ $$$$\mathrm{Show}\:\mathrm{this}\:\mathrm{equality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{when} \\ $$$$\mathrm{we}\:\mathrm{replace}\:\mathrm{p}\:\mathrm{by}\:\mathrm{p}+\mathrm{1} \\ $$
Answered by TANMAY PANACEA last updated on 05/Oct/20
![1+(n−1)2=2p+1 2n−1=2p+1→n=p+1 sum of (p+1) terms ((p+1)/2)[2×1+(p+1−1)2] (((p+1))/2)×[2p+2]=(p+1)^2 now sum of (p+1+1)terms from LHS (((p+2))/2)[2×1+(p+2−1)×2] =(((p+2))/2)×[2+2p+2]→(p+2)^2 RHS (p+1+1)^2 →(p+2)^2 hence proved](https://www.tinkutara.com/question/Q116688.png)
$$\mathrm{1}+\left({n}−\mathrm{1}\right)\mathrm{2}=\mathrm{2}{p}+\mathrm{1} \\ $$$$\mathrm{2}{n}−\mathrm{1}=\mathrm{2}{p}+\mathrm{1}\rightarrow{n}={p}+\mathrm{1} \\ $$$${sum}\:{of}\:\left({p}+\mathrm{1}\right)\:{terms} \\ $$$$\frac{{p}+\mathrm{1}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{1}+\left({p}+\mathrm{1}−\mathrm{1}\right)\mathrm{2}\right] \\ $$$$\frac{\left({p}+\mathrm{1}\right)}{\mathrm{2}}×\left[\mathrm{2}{p}+\mathrm{2}\right]=\left(\boldsymbol{{p}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{sum}}\:\boldsymbol{{of}}\:\left(\boldsymbol{{p}}+\mathrm{1}+\mathrm{1}\right)\boldsymbol{{terms}}\:\boldsymbol{{from}}\:\boldsymbol{{L}}{HS} \\ $$$$\frac{\left(\boldsymbol{{p}}+\mathrm{2}\right)}{\mathrm{2}}\left[\mathrm{2}×\mathrm{1}+\left(\boldsymbol{{p}}+\mathrm{2}−\mathrm{1}\right)×\mathrm{2}\right] \\ $$$$=\frac{\left(\boldsymbol{{p}}+\mathrm{2}\right)}{\mathrm{2}}×\left[\mathrm{2}+\mathrm{2}\boldsymbol{{p}}+\mathrm{2}\right]\rightarrow\left(\boldsymbol{{p}}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$${RHS}\:\left({p}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} \rightarrow\left(\boldsymbol{{p}}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\boldsymbol{{hence}}\:\boldsymbol{{proved}} \\ $$
