Question Number 110181 by Rio Michael last updated on 27/Aug/20
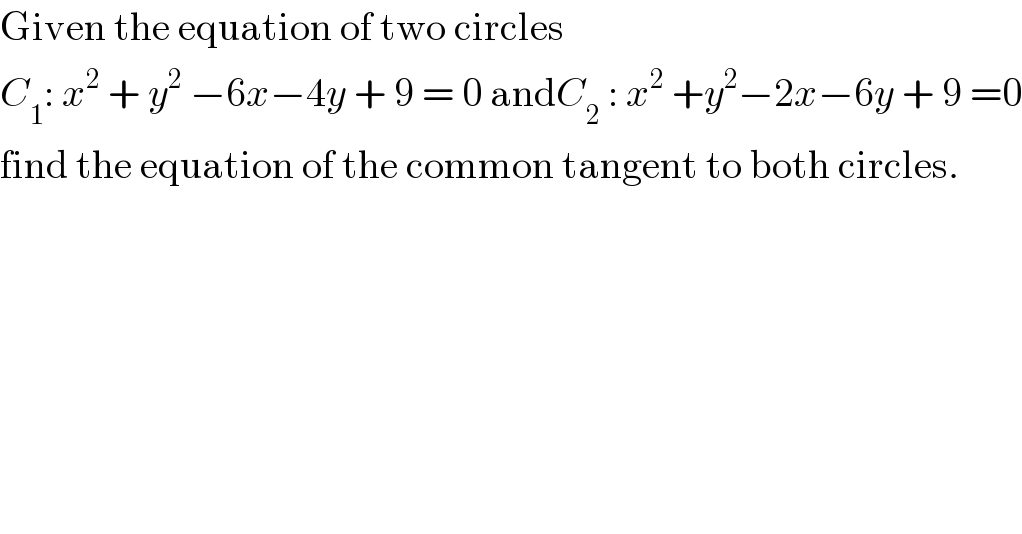
$$\mathrm{Given}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{two}\:\mathrm{circles} \\ $$$${C}_{\mathrm{1}} :\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:−\mathrm{6}{x}−\mathrm{4}{y}\:+\:\mathrm{9}\:=\:\mathrm{0}\:\mathrm{and}{C}_{\mathrm{2}} \::\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{6}{y}\:+\:\mathrm{9}\:=\mathrm{0} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{common}\:\mathrm{tangent}\:\mathrm{to}\:\mathrm{both}\:\mathrm{circles}. \\ $$
Commented by bemath last updated on 27/Aug/20
Commented by bemath last updated on 27/Aug/20
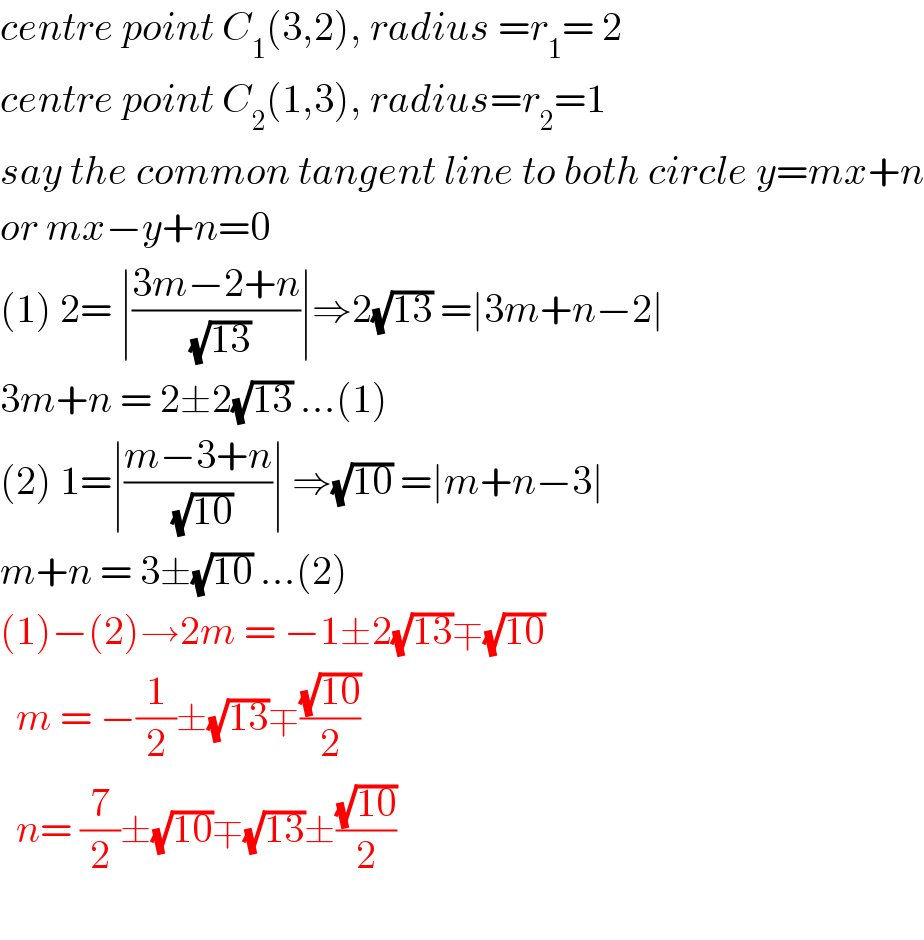
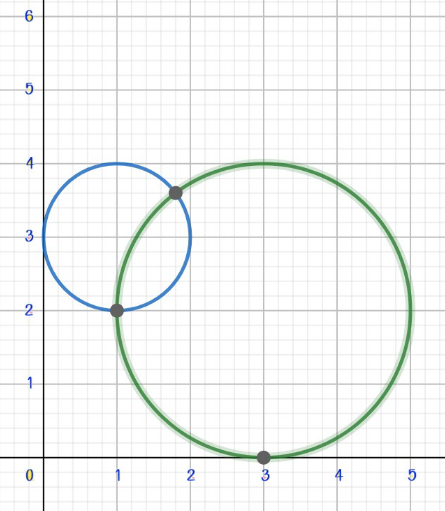
$${centre}\:{point}\:{C}_{\mathrm{1}} \left(\mathrm{3},\mathrm{2}\right),\:{radius}\:={r}_{\mathrm{1}} =\:\mathrm{2} \\ $$$${centre}\:{point}\:{C}_{\mathrm{2}} \left(\mathrm{1},\mathrm{3}\right),\:{radius}={r}_{\mathrm{2}} =\mathrm{1} \\ $$$${say}\:{the}\:{common}\:{tangent}\:{line}\:{to}\:{both}\:{circle}\:{y}={mx}+{n} \\ $$$${or}\:{mx}−{y}+{n}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}=\:\mid\frac{\mathrm{3}{m}−\mathrm{2}+{n}}{\:\sqrt{\mathrm{13}}}\mid\Rightarrow\mathrm{2}\sqrt{\mathrm{13}}\:=\mid\mathrm{3}{m}+{n}−\mathrm{2}\mid \\ $$$$\mathrm{3}{m}+{n}\:=\:\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{13}}\:…\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{1}=\mid\frac{{m}−\mathrm{3}+{n}}{\:\sqrt{\mathrm{10}}}\mid\:\Rightarrow\sqrt{\mathrm{10}}\:=\mid{m}+{n}−\mathrm{3}\mid \\ $$$${m}+{n}\:=\:\mathrm{3}\pm\sqrt{\mathrm{10}}\:…\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\rightarrow\mathrm{2}{m}\:=\:−\mathrm{1}\pm\mathrm{2}\sqrt{\mathrm{13}}\mp\sqrt{\mathrm{10}} \\ $$$$\:\:{m}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\mathrm{13}}\mp\frac{\sqrt{\mathrm{10}}}{\mathrm{2}} \\ $$$$\:\:{n}=\:\frac{\mathrm{7}}{\mathrm{2}}\pm\sqrt{\mathrm{10}}\mp\sqrt{\mathrm{13}}\pm\frac{\sqrt{\mathrm{10}}}{\mathrm{2}} \\ $$$$ \\ $$
