Question Number 109075 by Rio Michael last updated on 20/Aug/20

$$\mathrm{Given}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{twe}\:\mathrm{circles}\: \\ $$$${C}_{\mathrm{1}} \::\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:−\mathrm{6}{x}−\mathrm{4}{y}\:+\:\mathrm{9}\:=\:\mathrm{0}\:\mathrm{and}\:{C}_{\mathrm{2}} \::\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{6}{y}\:+\:\mathrm{9}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:{C}_{\mathrm{3}} \:\mathrm{which}\:\mathrm{passes}\:\mathrm{through}\:\mathrm{the}\:\mathrm{centre} \\ $$$$\mathrm{of}\:{C}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{through}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of}\:\mathrm{intersection}\:\mathrm{of}\:{C}_{\mathrm{1}} \:\mathrm{and}\:{C}_{\mathrm{2}} . \\ $$$$\left(\mathrm{b}\right)\:\mathrm{The}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{two}\:\mathrm{tangents}\:\mathrm{from}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{to}\:{C}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{the}\:\mathrm{lenght} \\ $$$$\mathrm{of}\:\mathrm{each}\:\mathrm{tangent}. \\ $$
Answered by john santu last updated on 21/Aug/20
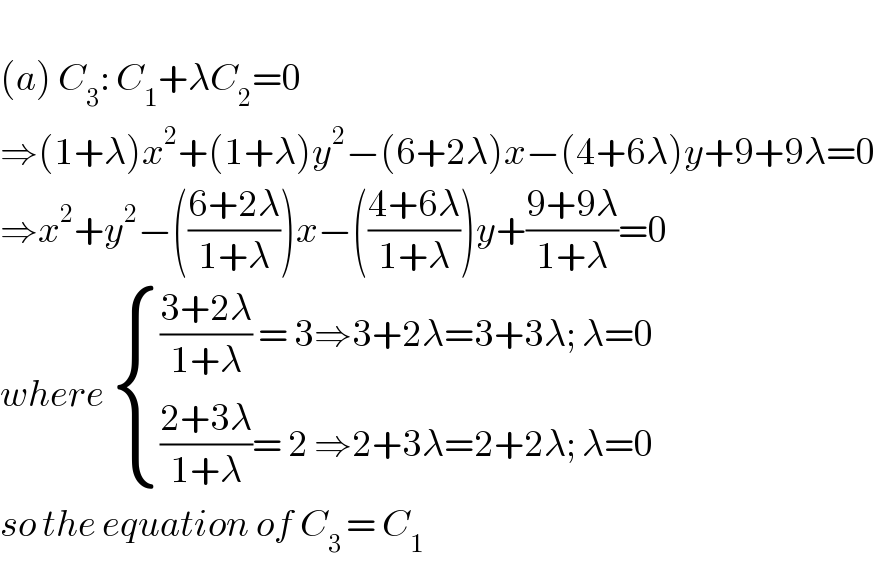
$$ \\ $$$$\left({a}\right)\:{C}_{\mathrm{3}} :\:{C}_{\mathrm{1}} +\lambda{C}_{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+\lambda\right){x}^{\mathrm{2}} +\left(\mathrm{1}+\lambda\right){y}^{\mathrm{2}} −\left(\mathrm{6}+\mathrm{2}\lambda\right){x}−\left(\mathrm{4}+\mathrm{6}\lambda\right){y}+\mathrm{9}+\mathrm{9}\lambda=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\left(\frac{\mathrm{6}+\mathrm{2}\lambda}{\mathrm{1}+\lambda}\right){x}−\left(\frac{\mathrm{4}+\mathrm{6}\lambda}{\mathrm{1}+\lambda}\right){y}+\frac{\mathrm{9}+\mathrm{9}\lambda}{\mathrm{1}+\lambda}=\mathrm{0} \\ $$$${where}\:\begin{cases}{\frac{\mathrm{3}+\mathrm{2}\lambda}{\mathrm{1}+\lambda}\:=\:\mathrm{3}\Rightarrow\mathrm{3}+\mathrm{2}\lambda=\mathrm{3}+\mathrm{3}\lambda;\:\lambda=\mathrm{0}}\\{\frac{\mathrm{2}+\mathrm{3}\lambda}{\mathrm{1}+\lambda}=\:\mathrm{2}\:\Rightarrow\mathrm{2}+\mathrm{3}\lambda=\mathrm{2}+\mathrm{2}\lambda;\:\lambda=\mathrm{0}}\end{cases} \\ $$$${so}\:{the}\:{equation}\:{of}\:{C}_{\mathrm{3}\:} =\:{C}_{\mathrm{1}} \: \\ $$
Commented by Rio Michael last updated on 21/Aug/20

$$\mathrm{sir}\:\mathrm{fourth}\:\mathrm{and}\:\mathrm{fifth}\:\mathrm{steps}\:\mathrm{not}\:\mathrm{understood}. \\ $$
Commented by Rio Michael last updated on 21/Aug/20
$$\mathrm{please}\:\mathrm{sir},\:\left(\mathrm{b}\:\right)\:\mathrm{part} \\ $$
