Question Number 90099 by Rio Michael last updated on 21/Apr/20
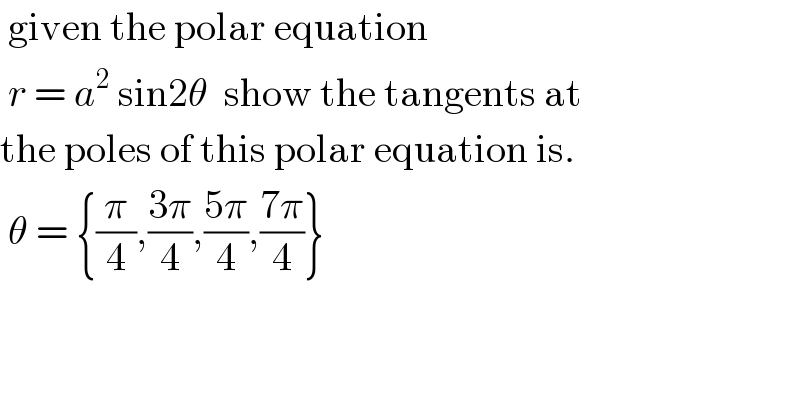
$$\:\mathrm{given}\:\mathrm{the}\:\mathrm{polar}\:\mathrm{equation} \\ $$$$\:{r}\:=\:{a}^{\mathrm{2}} \:\mathrm{sin2}\theta\:\:\mathrm{show}\:\mathrm{the}\:\mathrm{tangents}\:\mathrm{at}\: \\ $$$$\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\mathrm{this}\:\mathrm{polar}\:\mathrm{equation}\:\mathrm{is}. \\ $$$$\:\theta\:=\:\left\{\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}},\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}}\right\} \\ $$
Commented by jagoll last updated on 21/Apr/20
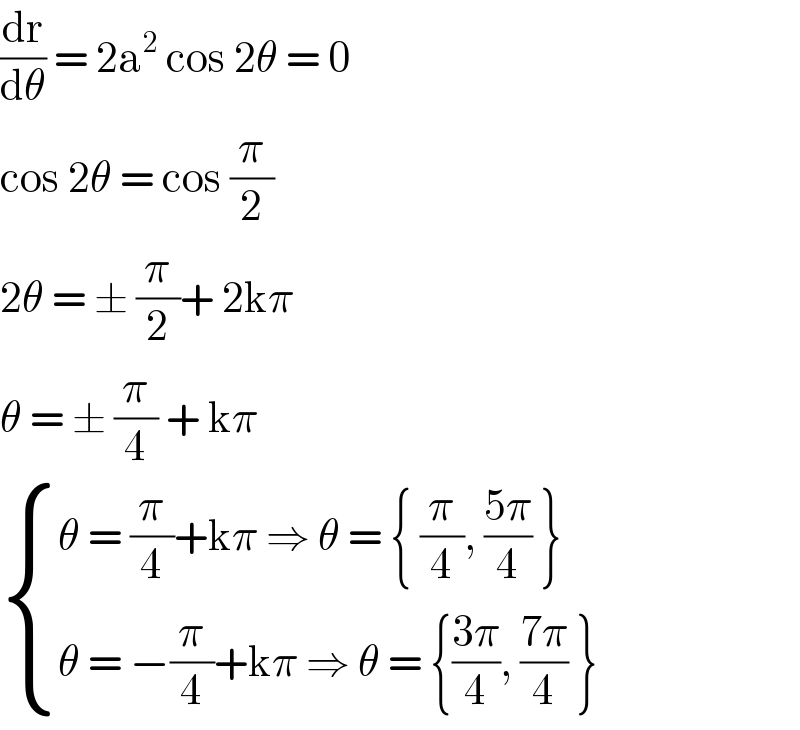
$$\frac{\mathrm{dr}}{\mathrm{d}\theta}\:=\:\mathrm{2a}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{2}\theta\:=\:\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta\:=\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{2}\theta\:=\:\pm\:\frac{\pi}{\mathrm{2}}+\:\mathrm{2k}\pi \\ $$$$\theta\:=\:\pm\:\frac{\pi}{\mathrm{4}}\:+\:\mathrm{k}\pi \\ $$$$\begin{cases}{\theta\:=\:\frac{\pi}{\mathrm{4}}+\mathrm{k}\pi\:\Rightarrow\:\theta\:=\:\left\{\:\frac{\pi}{\mathrm{4}},\:\frac{\mathrm{5}\pi}{\mathrm{4}}\:\right\}}\\{\theta\:=\:−\frac{\pi}{\mathrm{4}}+\mathrm{k}\pi\:\Rightarrow\:\theta\:=\:\left\{\frac{\mathrm{3}\pi}{\mathrm{4}},\:\frac{\mathrm{7}\pi}{\mathrm{4}}\:\right\}}\end{cases} \\ $$
Commented by Rio Michael last updated on 21/Apr/20
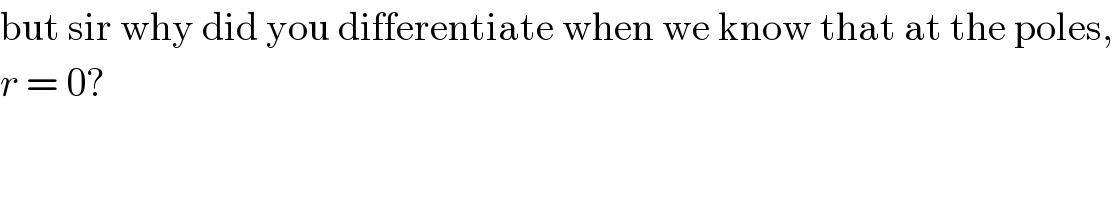
$$\mathrm{but}\:\mathrm{sir}\:\mathrm{why}\:\mathrm{did}\:\mathrm{you}\:\mathrm{differentiate}\:\mathrm{when}\:\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{at}\:\mathrm{the}\:\mathrm{poles}, \\ $$$${r}\:=\:\mathrm{0}? \\ $$
