Menu Close

Given-three-function-f-x-g-x-and-h-x-where-f-x-x-2-x-2-and-h-x-x-2-2x-1-If-f-x-x-3-g-x-x-3-h-x-x-3-then-the-value-of-lim-x-1-g-x-

Tinku Tara 0 Comments
Pin




Question Number 119253 by bemath last updated on 23/Oct/20
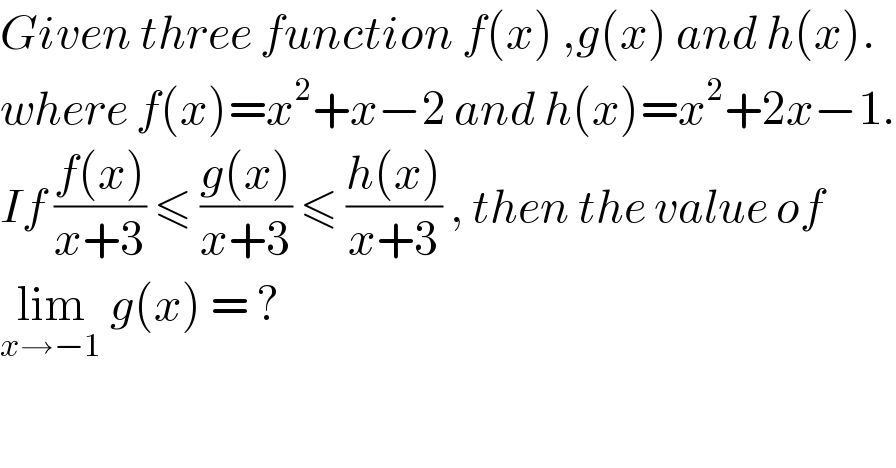
Given three function f(x) ,g(x) and h(x). where f(x)=x^2 +x−2 and h(x)=x^2 +2x−1. If ((f(x))/(x+3)) ≤ ((g(x))/(x+3)) ≤ ((h(x))/(x+3)) , then the value of lim_(x→−1) g(x) = ?
$${Given}\:{three}\:{function}\:{f}\left({x}\right)\:,{g}\left({x}\right)\:{and}\:{h}\left({x}\right). \\ $$$${where}\:{f}\left({x}\right)={x}^{\mathrm{2}} +{x}−\mathrm{2}\:{and}\:{h}\left({x}\right)={x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}. \\ $$$${If}\:\frac{{f}\left({x}\right)}{{x}+\mathrm{3}}\:\leqslant\:\frac{{g}\left({x}\right)}{{x}+\mathrm{3}}\:\leqslant\:\frac{{h}\left({x}\right)}{{x}+\mathrm{3}}\:,\:{then}\:{the}\:{value}\:{of} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:{g}\left({x}\right)\:=\:? \\ $$
Answered by benjo_mathlover last updated on 23/Oct/20
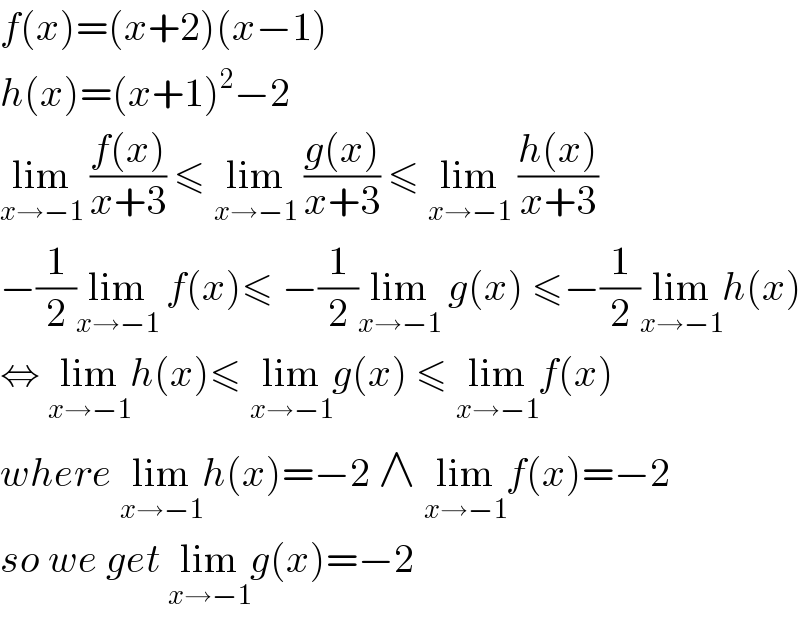
f(x)=(x+2)(x−1) h(x)=(x+1)^2 −2 lim_(x→−1) ((f(x))/(x+3)) ≤ lim_(x→−1) ((g(x))/(x+3)) ≤ lim_(x→−1) ((h(x))/(x+3)) −(1/2)lim_(x→−1) f(x)≤ −(1/2)lim_(x→−1) g(x) ≤−(1/2)lim_(x→−1) h(x) ⇔ lim_(x→−1) h(x)≤ lim_(x→−1) g(x) ≤ lim_(x→−1) f(x) where lim_(x→−1) h(x)=−2 ∧ lim_(x→−1) f(x)=−2 so we get lim_(x→−1) g(x)=−2
$${f}\left({x}\right)=\left({x}+\mathrm{2}\right)\left({x}−\mathrm{1}\right) \\ $$$${h}\left({x}\right)=\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)}{{x}+\mathrm{3}}\:\leqslant\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{{g}\left({x}\right)}{{x}+\mathrm{3}}\:\leqslant\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{{h}\left({x}\right)}{{x}+\mathrm{3}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:{f}\left({x}\right)\leqslant\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:{g}\left({x}\right)\:\leqslant−\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{h}\left({x}\right) \\ $$$$\Leftrightarrow\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{h}\left({x}\right)\leqslant\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{g}\left({x}\right)\:\leqslant\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{f}\left({x}\right) \\ $$$${where}\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{h}\left({x}\right)=−\mathrm{2}\:\wedge\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{f}\left({x}\right)=−\mathrm{2} \\ $$$${so}\:{we}\:{get}\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}{g}\left({x}\right)=−\mathrm{2} \\ $$
Answered by 1549442205PVT last updated on 23/Oct/20
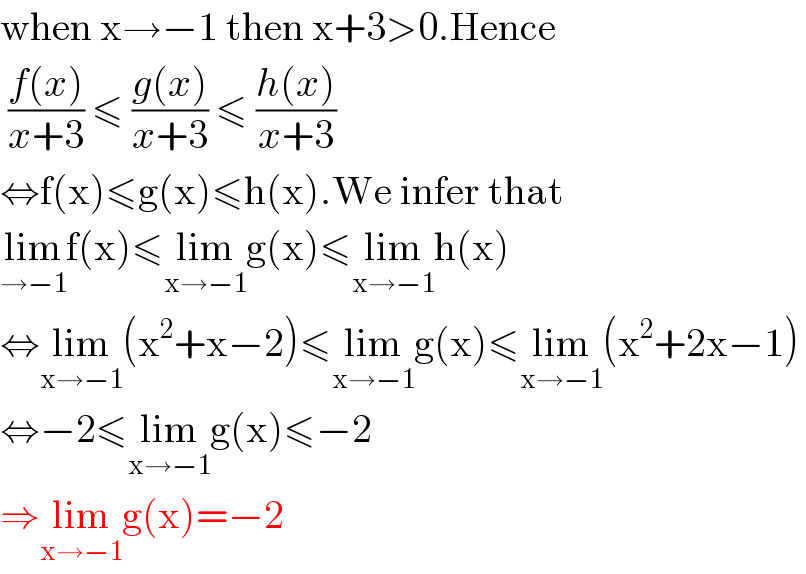
when x→−1 then x+3>0.Hence ((f(x))/(x+3)) ≤ ((g(x))/(x+3)) ≤ ((h(x))/(x+3)) ⇔f(x)≤g(x)≤h(x).We infer that lim_(→−1) f(x)≤lim_(x→−1) g(x)≤lim_(x→−1) h(x) ⇔lim_(x→−1) (x^2 +x−2)≤lim_(x→−1) g(x)≤lim_(x→−1) (x^2 +2x−1) ⇔−2≤lim_(x→−1) g(x)≤−2 ⇒lim_(x→−1) g(x)=−2
$$\mathrm{when}\:\mathrm{x}\rightarrow−\mathrm{1}\:\mathrm{then}\:\mathrm{x}+\mathrm{3}>\mathrm{0}.\mathrm{Hence} \\ $$$$\:\frac{{f}\left({x}\right)}{{x}+\mathrm{3}}\:\leqslant\:\frac{{g}\left({x}\right)}{{x}+\mathrm{3}}\:\leqslant\:\frac{{h}\left({x}\right)}{{x}+\mathrm{3}} \\ $$$$\Leftrightarrow\mathrm{f}\left(\mathrm{x}\right)\leqslant\mathrm{g}\left(\mathrm{x}\right)\leqslant\mathrm{h}\left(\mathrm{x}\right).\mathrm{We}\:\mathrm{infer}\:\mathrm{that} \\ $$$$\underset{\rightarrow−\mathrm{1}} {\mathrm{lim}f}\left(\mathrm{x}\right)\leqslant\underset{\mathrm{x}\rightarrow−\mathrm{1}} {\mathrm{lim}g}\left(\mathrm{x}\right)\leqslant\underset{\mathrm{x}\rightarrow−\mathrm{1}} {\mathrm{lim}h}\left(\mathrm{x}\right) \\ $$$$\Leftrightarrow\underset{\mathrm{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}\right)\leqslant\underset{\mathrm{x}\rightarrow−\mathrm{1}} {\mathrm{lim}g}\left(\mathrm{x}\right)\leqslant\underset{\mathrm{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}\right) \\ $$$$\Leftrightarrow−\mathrm{2}\leqslant\underset{\mathrm{x}\rightarrow−\mathrm{1}} {\mathrm{lim}g}\left(\mathrm{x}\right)\leqslant−\mathrm{2} \\ $$$$\Rightarrow\underset{\mathrm{x}\rightarrow−\mathrm{1}} {\mathrm{lim}g}\left(\mathrm{x}\right)=−\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *